Árboles de decisión (III)
Continuamos con la implementación en R de dos tipos de árboles de decisión, probablemente los algoritmos más empleados en Machine Learning. En este artículo construiremos un modelo rpart. En el artículo anterior planteamos un problema de clasificación, consistente en la predicción de posibles bajas (churn) de clientes de una operadora móvil. Cargamos allí los datos e hicimos una sencilla exploración de los mismos. En este vamos a preparar los datos para construir a continuación nuestro modelo de predicción. Evaluaremos después su rendimiento y, por último, veremos si podemos mejorarlo.
Preparación de los datos
Vamos a dividir nuestros datos en dos conjuntos:
Un train set, con el que construiremos nuestro modelo de árbol de decisión.
Un test set, sobre el que evaluaremos la eficiencia de nuestro modelo (esta técnica no es perfecta, ya veremos técnicas mejores).
Cargamos de nuevo los datos:
library(C50)
library(modeldata)
data(mlc_churn)
churn <- mlc_churnY realizaremos esta división tomando muestras aleatorias del total de los datos:
set.seed(127)
train_idx <- sample(nrow(churn), 0.9*nrow(churn))
churnTrain <- churn[train_idx,]
churnTest <- churn[-train_idx,]Hemos seleccionado aleatoriamente para el train setel 90% de los datos, dejando el 10% restante para el test set. Si lo hemos hecho bien, la distribución de la variable objetivo en ambos conjuntos de datos debe de ser parecida:
prop.table(table(churnTrain$churn))##
## yes no
## 0.1388889 0.8611111(Hay otras formas de hacer esta división de los datos, iremos viéndolas)
Creación del modelo
Como primer intento, vamos a crear un árbol de decisión rpart (si no tienes instalado el paquete: install packages("rpart")).
library(rpart)
rpart_churn_model <- rpart(formula = churn ~ .,
data = churnTrain)Con esta sentencia hemos creado un modelo que toma como base el train set y que trata de predecir la variable categórica objetivo churna partir de todas las demás variables (eso es lo que significa la fórmula churn ~ .)
Para mostrar los detalles del árbol:
rpart_churn_model## n= 4500
##
## node), split, n, loss, yval, (yprob)
## * denotes terminal node
##
## 1) root 4500 625 no (0.13888889 0.86111111)
## 2) total_day_minutes>=265.75 275 112 yes (0.59272727 0.40727273)
## 4) voice_mail_plan=no 208 51 yes (0.75480769 0.24519231)
## 8) total_eve_minutes>=167.3 152 13 yes (0.91447368 0.08552632) *
## 9) total_eve_minutes< 167.3 56 18 no (0.32142857 0.67857143)
## 18) total_day_minutes>=303.15 10 0 yes (1.00000000 0.00000000) *
## 19) total_day_minutes< 303.15 46 8 no (0.17391304 0.82608696) *
## 5) voice_mail_plan=yes 67 6 no (0.08955224 0.91044776) *
## 3) total_day_minutes< 265.75 4225 462 no (0.10934911 0.89065089)
## 6) number_customer_service_calls>=3.5 334 163 no (0.48802395 0.51197605)
## 12) total_day_minutes< 162.7 138 19 yes (0.86231884 0.13768116)
## 24) state=AK,AL,AR,CA,CT,DC,DE,FL,GA,ID,IN,KY,LA,MA,MD,ME,MI,MN,MO,MS,MT,NC,NE,NH,NJ,NM,NV,NY,OK,PA,SC,SD,TN,TX,UT,VT,WA,WI,WV 118 5 yes (0.95762712 0.04237288) *
## 25) state=CO,HI,IA,IL,KS,OH,OR,VA,WY 20 6 no (0.30000000 0.70000000) *
## 13) total_day_minutes>=162.7 196 44 no (0.22448980 0.77551020)
## 26) total_eve_minutes< 135.1 20 6 yes (0.70000000 0.30000000) *
## 27) total_eve_minutes>=135.1 176 30 no (0.17045455 0.82954545) *
## 7) number_customer_service_calls< 3.5 3891 299 no (0.07684400 0.92315600)
## 14) international_plan=yes 352 127 no (0.36079545 0.63920455)
## 28) total_intl_minutes>=13.05 64 0 yes (1.00000000 0.00000000) *
## 29) total_intl_minutes< 13.05 288 63 no (0.21875000 0.78125000)
## 58) total_intl_calls< 2.5 54 0 yes (1.00000000 0.00000000) *
## 59) total_intl_calls>=2.5 234 9 no (0.03846154 0.96153846) *
## 15) international_plan=no 3539 172 no (0.04860130 0.95139870)
## 30) total_day_minutes>=221.85 578 98 no (0.16955017 0.83044983)
## 60) total_eve_minutes>=242.35 110 48 yes (0.56363636 0.43636364)
## 120) voice_mail_plan=no 87 25 yes (0.71264368 0.28735632)
## 240) total_night_minutes>=174.2 65 9 yes (0.86153846 0.13846154) *
## 241) total_night_minutes< 174.2 22 6 no (0.27272727 0.72727273) *
## 121) voice_mail_plan=yes 23 0 no (0.00000000 1.00000000) *
## 61) total_eve_minutes< 242.35 468 36 no (0.07692308 0.92307692) *
## 31) total_day_minutes< 221.85 2961 74 no (0.02499156 0.97500844) *n indica el número de observaciones que alcanzan a cada nodo, loss el número de observaciones que se clasifican mal, yval es el valor de clasificación que se toma como referencia (“no”, en este caso) e yprob las probabilidades de ambas clases (el primer valor se refiere a la probabilidad de alcanzar el valor “no” y el segundo a la de alcanzar el valor “si”).
Por ejemplo, la primera línea es:
1) root 3333 483 no (0.14491449 0.85508551)Se trata del nodo raíz, con 3333 observaciones (como ya sabiamos) de las que 483 se han clasificado mal. El valor de referencia es “no”. La proporción de observaciones clasificadas como “no” es 0.14491449 y la de clasificadas como “si”, 0.85508551.
A partir del nodo raíz tenemos la primera decisión:
2) total_day_minutes>=264.45 211 84 yes (0.60189573 0.39810427)Es decir, la decisión de la primera bifurcación se toma mirando la variable total_day_minutes. Si es mayor o igual que 264.45, se clasifica como “yes”. A este nodo llegan 211 observaciones de las que 84 están mal clasificadas. El 0.60189573 se han clasificado como “yes” y el 0.39810427 (84/211) como “no”.
Nótese que el nodo 3 es la otra rama de la decisión:
3) total_day_minutes< 264.45 3122 356 no (0.11402947 0.88597053)Todo esto es más fácil verlo gráficamente:
plot(rpart_churn_model, uniform = TRUE, branch = 0.6, margin = 0.1)
text(rpart_churn_model, all = TRUE, use.n = TRUE, cex = .5)
plot(rpart_churn_model, uniform = TRUE, branch = 0.1, margin = 0.01)
text(rpart_churn_model, all = TRUE, use.n = TRUE, cex = .4)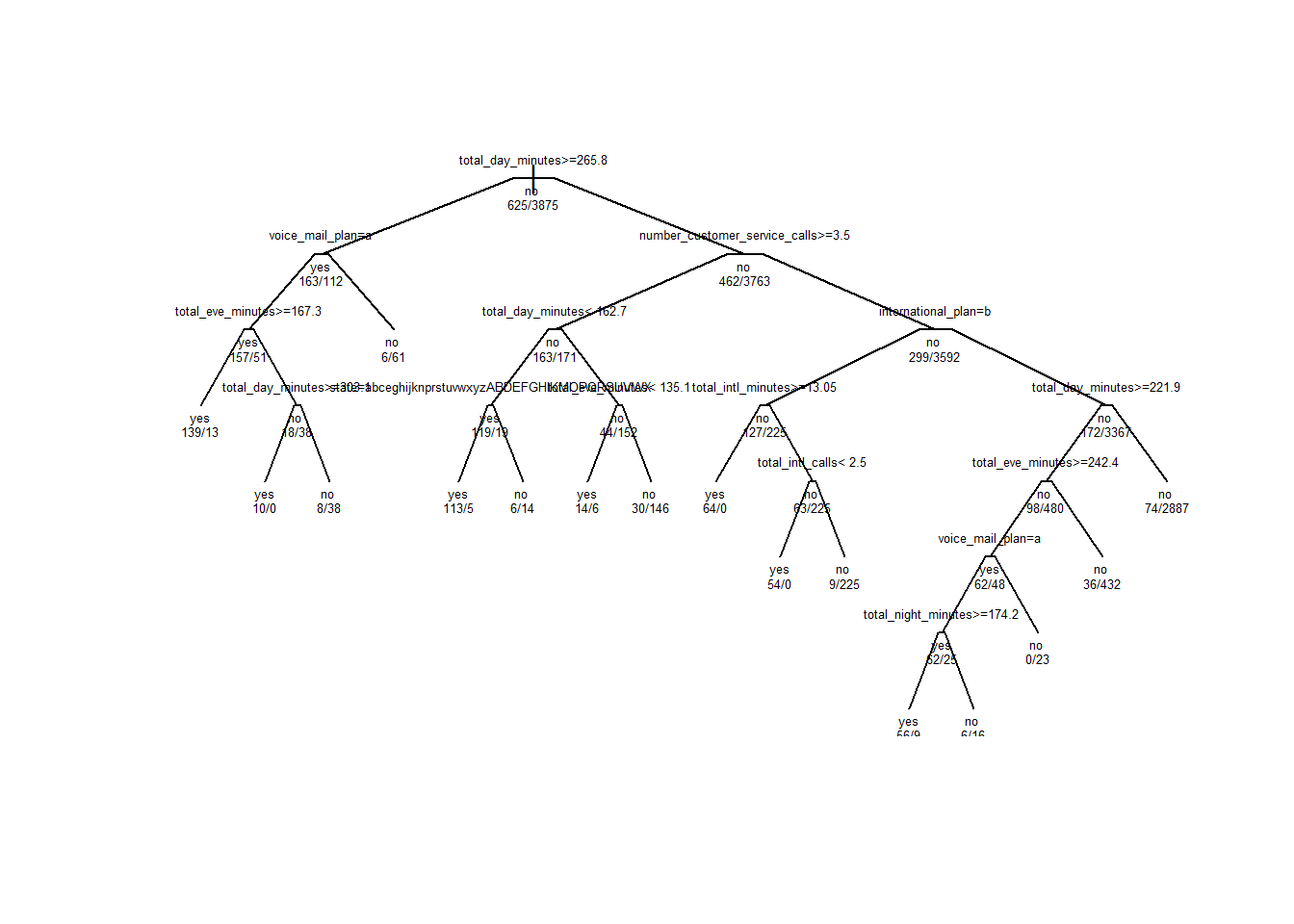
Para ver los parámetros de complejidad del modelo:
printcp(x= rpart_churn_model)##
## Classification tree:
## rpart(formula = churn ~ ., data = churnTrain)
##
## Variables actually used in tree construction:
## [1] international_plan number_customer_service_calls
## [3] state total_day_minutes
## [5] total_eve_minutes total_intl_calls
## [7] total_intl_minutes total_night_minutes
## [9] voice_mail_plan
##
## Root node error: 625/4500 = 0.13889
##
## n= 4500
##
## CP nsplit rel error xerror xstd
## 1 0.084800 0 1.0000 1.0000 0.037118
## 2 0.080000 2 0.8304 0.9392 0.036148
## 3 0.051200 4 0.6704 0.7200 0.032199
## 4 0.032000 7 0.4816 0.5264 0.027940
## 5 0.019733 8 0.4496 0.5024 0.027345
## 6 0.016000 11 0.3904 0.5008 0.027305
## 7 0.012800 13 0.3584 0.5056 0.027425
## 8 0.010000 15 0.3328 0.5104 0.027545Utilizaremos los parámetros de complejidad (CP) como una penalización para controlar el tamaño del árbol. En resumen, cuanto mayor es el parámetro de complejidad, menos decisiones contiene el árbol (nsplit). El valor rel error representa la desviación media del árbol al que se refiera dividida entre la desviación media del árbol nulo (nsplit = 0). El valor xerror es el valor medio estimado mediante un procedimiento de cross validation que ya veremos. xstd es el error estándar del error relativo.
La información sobre el CPse puede visualizar:
rpart::plotcp(rpart_churn_model, main = "size of tree", cex.main = .7)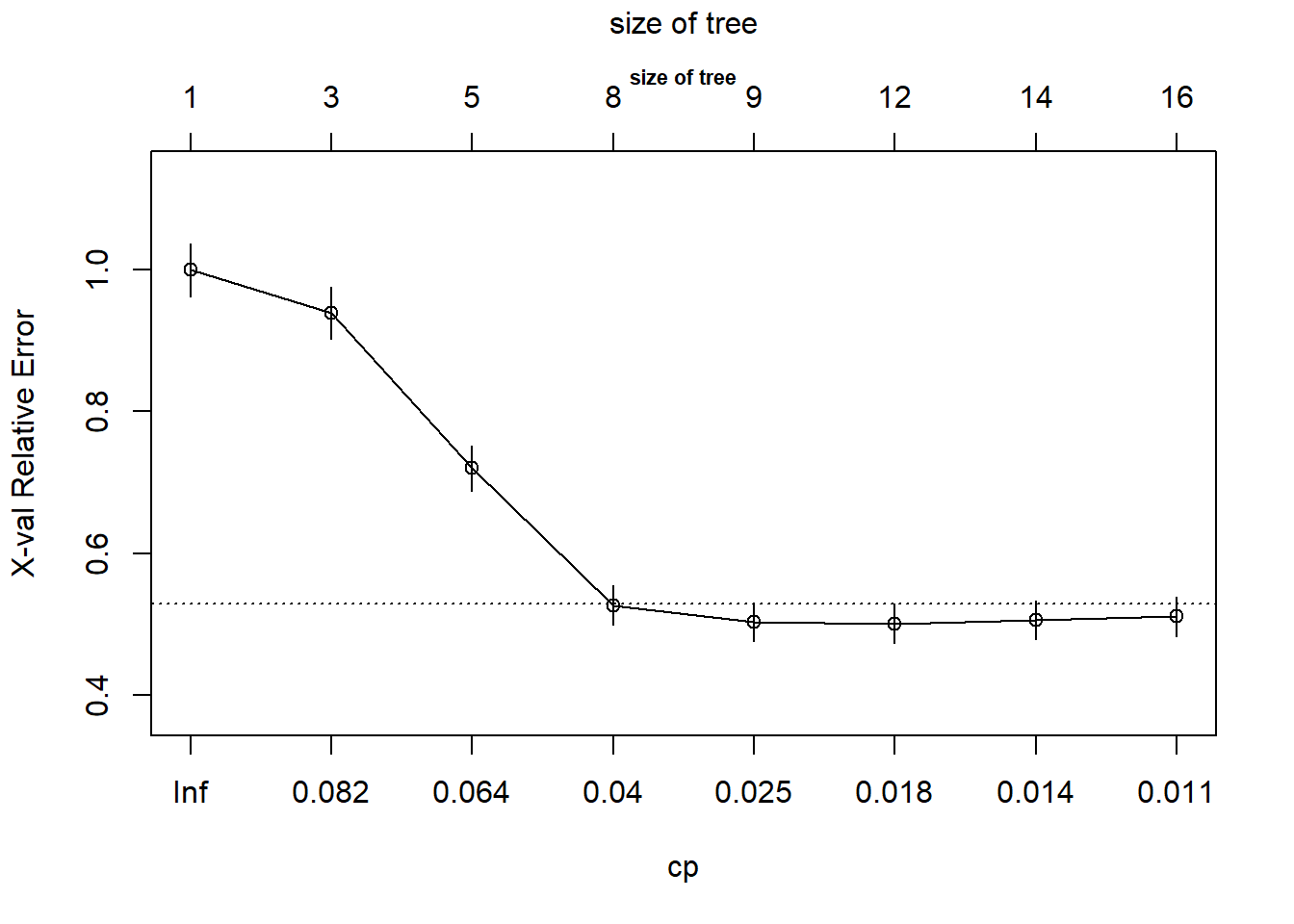
El eje x inferior representa el CP, el eje y es el error relativo y el eje x superior es el tamaño del árbol.
Rendimiento del modelo
Ahora que ya hemos construido nuestro modelo, podemos utilizarlo para predecir la categoría basándonos en nuevas observaciones. Pero antes de esto, veamos cuál es el poder de predicción de nuestro modelo utilizando los datos del test set.
Para hacer predicciones sobre nuestro test set:
rpart_predictions <- predict(object = rpart_churn_model,
newdata = churnTest,
type = "class")Y ahora usaremos la función table para crear una tabla de las clasificaciones realizadas:
table(churnTest$churn, rpart_predictions)## rpart_predictions
## yes no
## yes 52 30
## no 4 414Esta tabla nos dice que, de los 66 verdaderos “yes” en el test set, hemos acertado 41 pero 25 los hemos clasificado como “no”; y que de los verdaderos 434 “no” en el test set, 427 los hemos clasificado correctamente pero 7 los hemos clasificado como “yes”.
Esto se ve mejor con la función confusionMatrix del paquete caret:
library(caret)
cm <- confusionMatrix(data = rpart_predictions,
reference = churnTest$churn)
cm$table## Reference
## Prediction yes no
## yes 52 4
## no 30 414Al número total de aciertos lo llamamos Accuracy o exactitud:
Accuracy=52+41452+4+414+30=0.932
El porcentaje de falsos positivos es:
FP=452+4=0.3787879
Y el de falsos negativos:
FN=frac7427+7=0.016129
La sensibilidad (verdaderos positivos) es:
Sensitivity=1−FP=frac4141+25=0.6212121
Y la especificidad (verdaderos negativos):
Specificity=1−FN=frac427427+7=0.983871
Estas son algunas de las medidas que se utilizan para estimar el rendimiento de un modelo de clasificación. Más adelante veremos este temas con más detenimiento y profundidad.
Mejorando el modelo: podar el árbol
Uno de los principales problemas de los árboles de decisión es su tendencia al overfitting: se ajustan tan bien al train set que capturan no sólo la “señal” existente en el train set, sino tambien el “ruido”, de manera que su rendimiento es mucho peor con el test set (cuando realizan predicciones sobre observaciones que no se han visto durante el entrenamiento).
Para reducir este problema, y para intentar mejorar la accuracy, se recurre a una técnica conocida como prunning o “podado” del árbol: eliminaremos las ramas del árbol que no contribuyen a capturar “señal”.
En el caso de los árboles rpart, utiliaremos el CP para realizar el podado.
Primero buscaremos el menor error de cross-validation (xerror) en el modelo. Para ello acudiremos a la tabla que ya hemos visto antes:
rpart_churn_model$cptable## CP nsplit rel error xerror xstd
## 1 0.08480000 0 1.0000 1.0000 0.03711843
## 2 0.08000000 2 0.8304 0.9392 0.03614829
## 3 0.05120000 4 0.6704 0.7200 0.03219938
## 4 0.03200000 7 0.4816 0.5264 0.02794035
## 5 0.01973333 8 0.4496 0.5024 0.02734501
## 6 0.01600000 11 0.3904 0.5008 0.02730470
## 7 0.01280000 13 0.3584 0.5056 0.02742541
## 8 0.01000000 15 0.3328 0.5104 0.02754540¿En qué fila de la tabla se encuentra el mínimo CP?
row_min_xerror <- which.min(rpart_churn_model$cptable[, "xerror"])
row_min_xerror## 6
## 6El CP correspondiente es:
CP_min_xerror <- rpart_churn_model$cptable[row_min_xerror, "CP"]
CP_min_xerror## [1] 0.016Ahora podamos el árbol:
rpart_churn_prunned_model <- prune(tree = rpart_churn_model,
cp = CP_min_xerror)Visualizamos el nuevo árbol:
plot(rpart_churn_prunned_model, uniform = TRUE, branch = 0.6, margin = 0.01)
text(rpart_churn_prunned_model, all = TRUE, use.n = TRUE, cex = .7)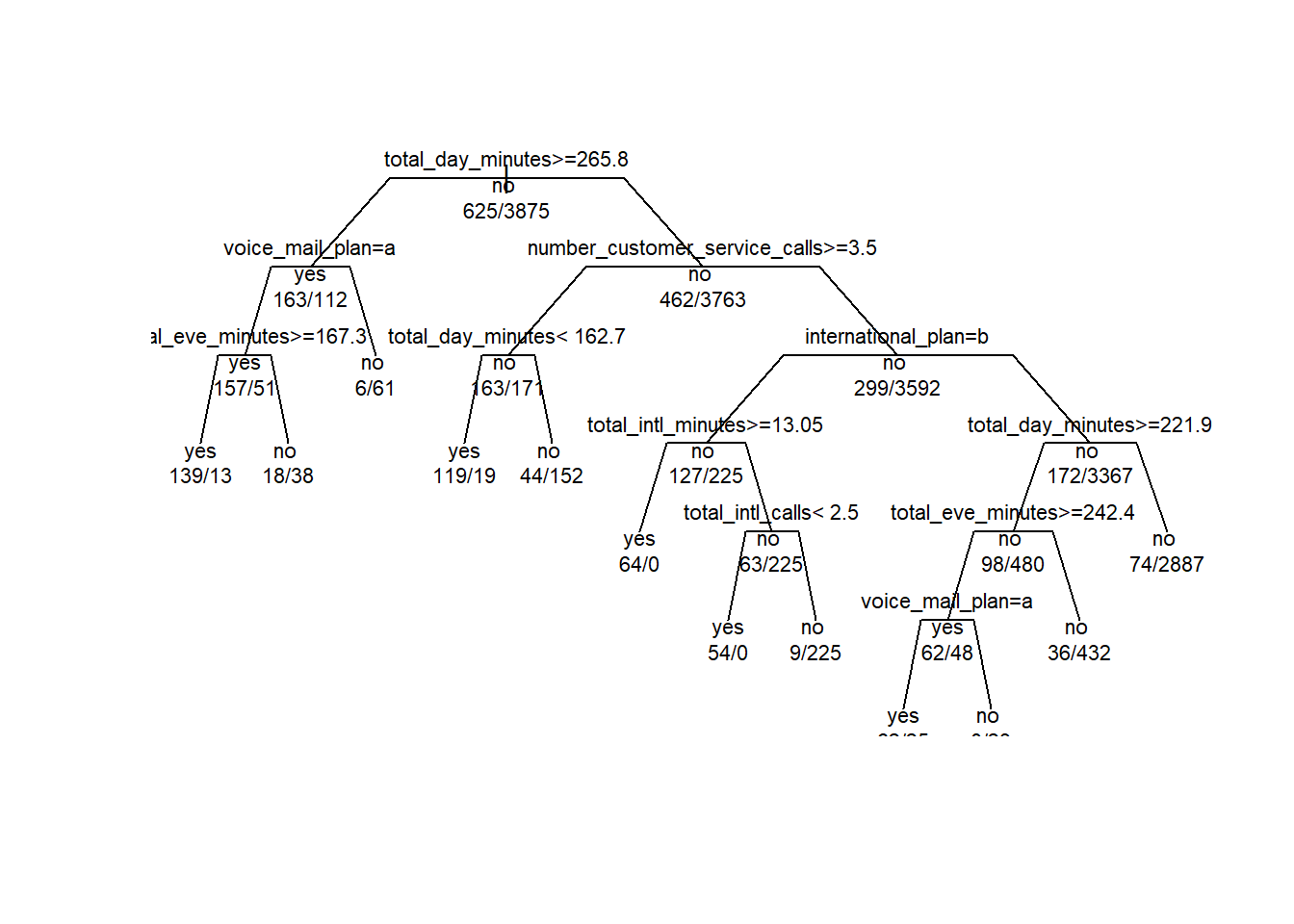
Y comprobamos su rendimiento:
rpart_prunned_predictions <- predict(object = rpart_churn_prunned_model,
newdata = churnTest,
type = "class")
confusionMatrix(data = rpart_prunned_predictions,
reference = churnTest$churn)$table## Reference
## Prediction yes no
## yes 55 6
## no 27 412Comparemos los resultados:
| Indicador | Árbol Completo | Árbol podado |
|---|---|---|
| Accuracy | 0.948 | 0.942 |
| FP | 0.3333333 | 0.4333333 |
| FN | 0.0136364 | 0.0068182 |
| Sensitivity | 0.6666667 | 0.5666667 |
| Specificity | 0.9863636 | 0.9931818 |
¿Cuáles son las diferencias?
El nuevo árbol tiene un nivel menos que el originario, es algo más sencillo.
La accuracy ha disminuido ligeramente.
Los falsos positivos han aumentado pero han disminuido los falsos negativos.
Los verdaderos positivos han disminuido pero han aumentado los verdaderos negativos.
¿Qué modelo es mejor? Pues depende. Depende de lo que queramos. Aquí si que no pueden ayudarnos los sistemas automáticos, es una decisión humana.
En este caso no parece demasiado interesante (¿recuerdas la pregunta original? Era: ¿podemos prever qué clientes se van a ir?) no parece apropiado dejar escapar verdaderos positivos… aunque sea a costa de considerar en riesgo a más clientes de los que verdaderamente van a irse…
En mi opinión, en este caso, aunque el árbol podado sea más robusto al haber eliminado decisiones que podrían aumentar el riesgo de overfitting, deberíamos quedarnos con el árbol original.
En el siguiente artículo aplicaremos a este mismo problema otro tipo de árbol de decisión, el C5.0.
Para terminar, solo resumir los pasos que hemos seguido:
Obtención de los datos
Exploración y preparación de los datos
Construcción del modelo
Evaluación de su rendimiento
Posibilidades de mejora



