Machine Learning Ensembles II
Como nos propusimos en el artículo anterior, vamos a preparar un primer ensemble entrenando un random forest, un svm tipo radial y un xgbm tipo tree como modelos de primer nivel.
Para construirlos vamos a aprovechar las facilidades del paquete caret. Por ejemplo, nos permitirá validar los modelos construidos mediante cross validation, es decir, usando solo el train set sin necesidad de disponer de un data set específico para validación.
Como modelos de 2º nivel vamos a probar con una media, una media ponderada y una votación.
Como estos modelos de segundo nivel no los construiremos con caret, necesitaremos un data set específico para validarlos.
El código lo podéis encontrar en github.
En primer lugar, vamos a cargar los datos:
library(C50)
library(modeldata)
data(mlc_churn)
churn <- mlc_churnHemos cargado un train set (churnTrain) y un test set (churnTest). El primero lo usaremos para construir y validar los modelos y el segundo será la “prueba de fuego”, es decir, datos que no habremos visto nunca durante la construcción de los modelos y que utilizaremos como datos en condiciones reales.
No vamos a repetir aquí la exploración de los datos que ya hemos hecho en los posts Arboles de Decisión I, II, III y IV, sino que vamos a ir directamente a la construcción del ensemble.
Preparemos los datos y dividamos churnTrain en un train set y un validation set:
# Variables target y predictoras (features)
target <- "churn"
predictoras <- names(churn)[names(churn) != target]
# Convertimos factors a integer para que no nos de problemas con svm ni xgbm
for (v in predictoras) {
if (is.factor(churn[, v])) {
newName <- paste0("F_", v)
names(churn)[which(names(churn) == v)] <- newName
churn[, v] <- unclass(churn[, newName])
}
}
set.seed(127)
train_idx <- sample(nrow(churn), 0.9*nrow(churn))
churnTrain <- churn[train_idx,]
churnTest <- churn[-train_idx,]
rm(churn)
library(caret)
set.seed(123)
train_idx <- createDataPartition(churnTrain$churn, p = 0.75, list = FALSE)
churn_train <- churnTrain[ train_idx, c(target, predictoras)]
churn_valid <- churnTrain[-train_idx, c(target, predictoras)]Preparemos ahora los controles que vamos a utilizar al construir nuestros modelos:
trControl <- trainControl(
# 5-fold Cross Validation
method = "cv",
number = 5,
# Save the predictions for the optimal tuning
# parameters
savePredictions = 'final',
# Class probabilities will be computed along with
# predicted values in each resample
classProbs = TRUE
)Construimos nuestros tres modelos de primer nivel:
f <- as.formula(paste0(target, "~ ."))
model_rf <- train(f, churn_train,
method = "rf",
trControl = trControl,
tuneLength = 3)
model_svm <- train(f, churn_train,
method = "svmRadial",
trControl = trControl,
tuneLength = 3)
model_xgbm <- train(f, churn_train,
method = "xgbTree",
trControl = trControl,
tuneLength = 3)Veamos la performance de cada uno de los 3 modelos y comparemos (nótese que las medidas de rendimiento se toman mediante cross validation sobre el training set, no necesitamos acudir al validation set):
resamps <- resamples(list(rf = model_rf, svm = model_svm, xgbm = model_xgbm))
summary(resamps)##
## Call:
## summary.resamples(object = resamps)
##
## Models: rf, svm, xgbm
## Number of resamples: 5
##
## Accuracy
## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## rf 0.9482249 0.9556213 0.9569733 0.9564602 0.9600000 0.9614815 0
## svm 0.9274074 0.9318519 0.9319527 0.9315757 0.9333333 0.9333333 0
## xgbm 0.9406528 0.9497041 0.9600000 0.9558597 0.9644444 0.9644970 0
##
## Kappa
## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## rf 0.7660206 0.7961112 0.8004094 0.8037613 0.8228811 0.8333840 0
## svm 0.6522265 0.6718383 0.6806162 0.6752822 0.6817326 0.6899972 0
## xgbm 0.7173352 0.7647589 0.8211885 0.7970728 0.8387789 0.8433026 0bwplot(resamps)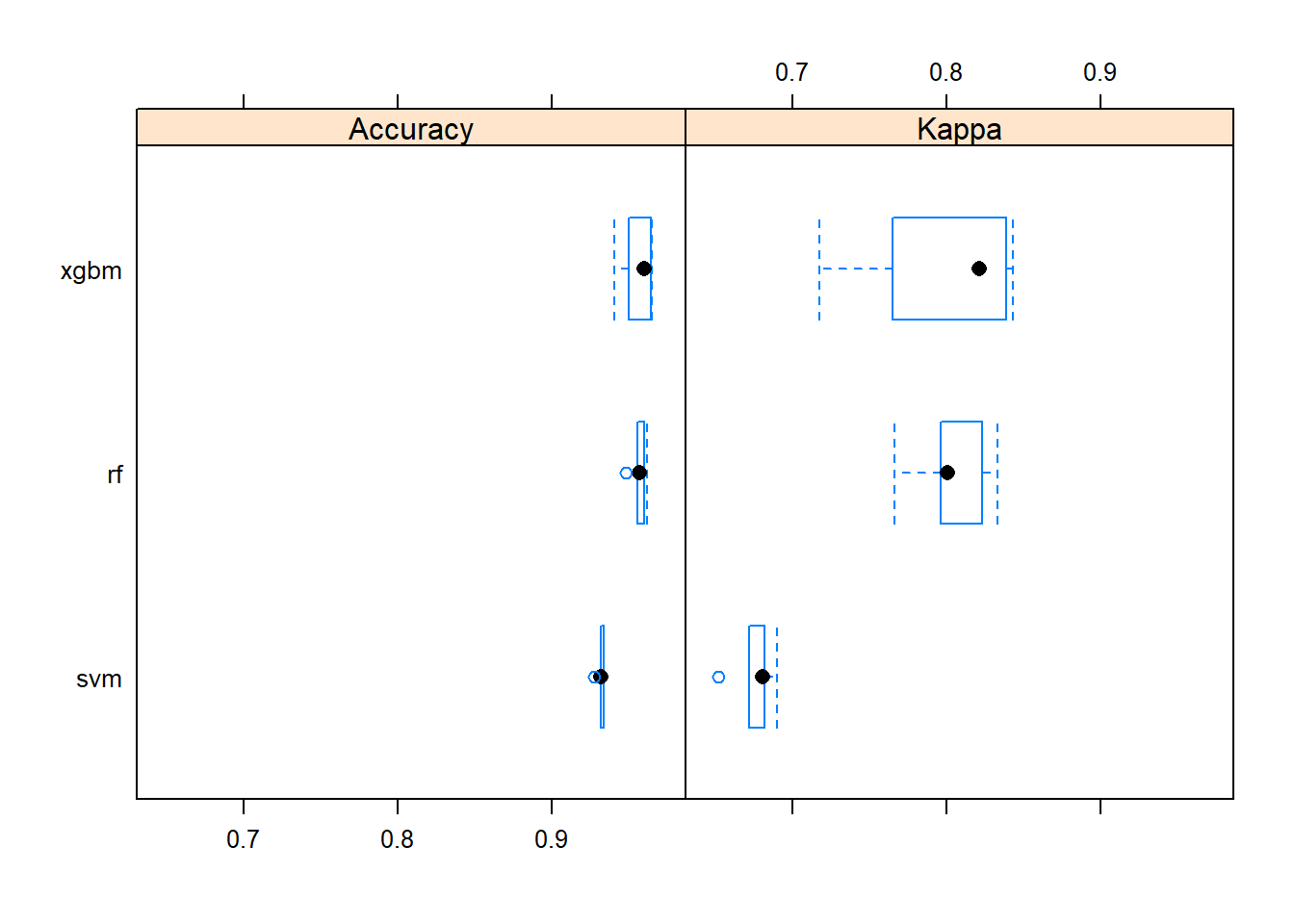
Los tres modelos presentan una elevada accuracy (rf = 0.9532, svm = 0.9212, xgbm = 0.9504), aunque la kappa del svm es notablemente menor que la de los otros dos.
diffs <- diff(resamps)
summary(diffs)##
## Call:
## summary.diff.resamples(object = diffs)
##
## p-value adjustment: bonferroni
## Upper diagonal: estimates of the difference
## Lower diagonal: p-value for H0: difference = 0
##
## Accuracy
## rf svm xgbm
## rf 0.0248845 0.0006005
## svm 0.0003744 -0.0242840
## xgbm 1.0000000 0.0183899
##
## Kappa
## rf svm xgbm
## rf 0.128479 0.006688
## svm 0.0006129 -0.121791
## xgbm 1.0000000 0.0175165Además xgbm y rf dan resultados completamente correlados.
A partir de esto podríamos quedarnos con svm y elegir entre xgbm y rf para, a continuación, tratar de añadir más modelos poco correlados con los dos elegidos.
Sin embargo, vamos a darnos por satisfechos con los tres modelos para continuar con el ejemplo y construir algunos modelos de nivel 2.
Lo primero que necesito son las nuevas variables predictoras, esta vez de segundo nivel. Nótese que a partir de ahora tenemos que utilizar el validation set para validar los modelos de segundo nivel.
# Utilizamos los modelos de 1er nivel para predecir
churn_valid$pred_rf <- predict(object = model_rf,
churn_valid[ , predictoras])
churn_valid$pred_svm <- predict(object = model_svm,
churn_valid[ , predictoras])
churn_valid$pred_xgbm <- predict(object = model_xgbm,
churn_valid[ , predictoras])
# Y sus probabilidades
churn_valid$pred_rf_prob <- predict(object = model_rf,
churn_valid[,predictoras],
type='prob')
churn_valid$pred_svm_prob <- predict(object = model_svm,
churn_valid[,predictoras],
type='prob')
churn_valid$pred_xgbm_prob <- predict(object = model_xgbm,
churn_valid[,predictoras],
type='prob')Empecemos con una simple media:
## PROMEDIO
# Calculamos la media de las predictoras de primer nivel
churn_valid$pred_avg <- (churn_valid$pred_rf_prob$yes +
churn_valid$pred_svm_prob$yes +
churn_valid$pred_xgbm_prob$yes) / 3
# Dividimos las clases binarias en p = 0.5
churn_valid$pred_avg <- as.factor(ifelse(churn_valid$pred_avg > 0.5,
'yes', 'no'))Ahora la media ponderada. Como el orden de los modelos de primer nivel, según su Accuracy, era rf y xgbm (empatados) seguidos por svm, vamos a asignarle pesos 0.25, 0.25 y 0.5:
## MEDIA PONDERADA
# Calculamos la media ponderada de las predictoras de primer nivel
churn_valid$pred_weighted_avg <- (churn_valid$pred_rf_prob$yes * 0.25) +
(churn_valid$pred_xgbm_prob$yes * 0.25) +
(churn_valid$pred_svm_prob$yes * 0.5)
# Dividimos las clases binarias en p = 0.5
churn_valid$pred_weighted_avg <- as.factor(ifelse(churn_valid$pred_weighted_avg > 0.5,
'yes', 'no'))Por último, hagamos que los modelos “voten”:
## VOTACIÓN
# La mayoría gana
predictoras2N <- c("pred_rf", "pred_xgbm", "pred_svm")
churn_valid$pred_majority <-
as.factor(apply(churn_valid[, predictoras2N],
1,
function(x) {
if (sum(x == "yes") > sum(x == "no"))
return("yes")
else
return("no")
}))Comparemos resultados contra el test set:
## PROMEDIO
confusionMatrix(churn_valid$churn, churn_valid$pred_avg)## Confusion Matrix and Statistics
##
## Reference
## Prediction no yes
## no 962 6
## yes 42 114
##
## Accuracy : 0.9573
## 95% CI : (0.9438, 0.9683)
## No Information Rate : 0.8932
## P-Value [Acc > NIR] : 5.071e-15
##
## Kappa : 0.8022
##
## Mcnemar's Test P-Value : 4.376e-07
##
## Sensitivity : 0.9582
## Specificity : 0.9500
## Pos Pred Value : 0.9938
## Neg Pred Value : 0.7308
## Prevalence : 0.8932
## Detection Rate : 0.8559
## Detection Prevalence : 0.8612
## Balanced Accuracy : 0.9541
##
## 'Positive' Class : no
## ## MEDIA PONDERADA
confusionMatrix(churn_valid$churn, churn_valid$pred_weighted_avg)## Confusion Matrix and Statistics
##
## Reference
## Prediction no yes
## no 958 10
## yes 43 113
##
## Accuracy : 0.9528
## 95% CI : (0.9388, 0.9645)
## No Information Rate : 0.8906
## P-Value [Acc > NIR] : 8.075e-14
##
## Kappa : 0.7835
##
## Mcnemar's Test P-Value : 1.105e-05
##
## Sensitivity : 0.9570
## Specificity : 0.9187
## Pos Pred Value : 0.9897
## Neg Pred Value : 0.7244
## Prevalence : 0.8906
## Detection Rate : 0.8523
## Detection Prevalence : 0.8612
## Balanced Accuracy : 0.9379
##
## 'Positive' Class : no
## ## VOTACIÓN
confusionMatrix(churn_valid$churn, churn_valid$pred_majority)## Confusion Matrix and Statistics
##
## Reference
## Prediction no yes
## no 964 4
## yes 42 114
##
## Accuracy : 0.9591
## 95% CI : (0.9458, 0.9699)
## No Information Rate : 0.895
## P-Value [Acc > NIR] : 2.681e-15
##
## Kappa : 0.8093
##
## Mcnemar's Test P-Value : 4.888e-08
##
## Sensitivity : 0.9583
## Specificity : 0.9661
## Pos Pred Value : 0.9959
## Neg Pred Value : 0.7308
## Prevalence : 0.8950
## Detection Rate : 0.8577
## Detection Prevalence : 0.8612
## Balanced Accuracy : 0.9622
##
## 'Positive' Class : no
## Como se ve, los modelos de segundo nivel media y votación dan resultados ligeramente mejores que los de primer nivel. Podríamos elegir cualquiera de los dos.
Supongamos que elegimos el modelo de votación. ¿Qué nos quedaría por hacer ahora? Pues construir el modelo final. Para ello, construiriamos los modelos definitivos de primer nivel utilizando esta vez todos los datos de entrenamiento (es decir, churnTrain completo) y los parámetros que optimizados por caret.
# Parámetros a utilizar
model_rf$bestTune## mtry
## 2 10model_svm$bestTune## sigma C
## 3 0.03400684 1model_xgbm$bestTune## nrounds max_depth eta gamma colsample_bytree min_child_weight subsample
## 40 50 3 0.3 0 0.6 1 0.75trControl <- trainControl(
method = "none",
# Class probabilities will be computed along with
# predicted values in each resample
classProbs = TRUE
)
best_model_rf <- train(f, churnTrain,
method = "rf",
trControl = trControl,
tuneGrid = model_rf$bestTune)
best_model_svm <- train(f, churnTrain,
method = "svmRadial",
trControl = trControl,
tuneGrid = model_svm$bestTune)
best_model_xgbm <- train(f, churnTrain,
method = "xgbTree",
trControl = trControl,
tuneGrid = model_xgbm$bestTune)Y ahora predeciriamos el test set con nuestro modelo de votación:
churn_test <- churnTest
# Utilizamos los modelos de 1er nivel para predecir
churn_test$pred_rf <- predict(object = model_rf,
churn_test[ , predictoras])
churn_test$pred_svm <- predict(object = model_svm,
churn_test[ , predictoras])
churn_test$pred_xgbm <- predict(object = model_xgbm,
churn_test[ , predictoras])
# Y sus probabilidades
churn_test$pred_rf_prob <- predict(object = model_rf,
churn_test[,predictoras],
type='prob')
churn_test$pred_svm_prob <- predict(object = model_svm,
churn_test[,predictoras],
type='prob')
churn_test$pred_xgbm_prob <- predict(object = model_xgbm,
churn_test[,predictoras],
type='prob')
churn_test$pred_majority <-
as.factor(apply(churn_test[, predictoras2N],
1,
function(x) {
if (sum(x == "yes") > sum(x == "no"))
return("yes")
else
return("no")
}))Y estos son los resultados:
## VOTACIÓN
confusionMatrix(churn_test$churn, churn_test$pred_majority)## Confusion Matrix and Statistics
##
## Reference
## Prediction no yes
## no 416 2
## yes 24 58
##
## Accuracy : 0.948
## 95% CI : (0.9247, 0.9658)
## No Information Rate : 0.88
## P-Value [Acc > NIR] : 1.736e-07
##
## Kappa : 0.7874
##
## Mcnemar's Test P-Value : 3.814e-05
##
## Sensitivity : 0.9455
## Specificity : 0.9667
## Pos Pred Value : 0.9952
## Neg Pred Value : 0.7073
## Prevalence : 0.8800
## Detection Rate : 0.8320
## Detection Prevalence : 0.8360
## Balanced Accuracy : 0.9561
##
## 'Positive' Class : no
## Realmente son unos muy buenos resultados. Hasta ahora no habíamos visto estos datos de churnTest para nada, es la primera vez que nuestros modelos se enfrentan a ellos. Y han obtenido una performance comparable a la obtenida en el proceso de entrenamiento, cuando normalmente se obtiene inferior performance con los datos “nuevos” del test set que con los del train set, como es lógico.
