Machine Learning Ensembles III
En este artículo vamos a crear un modelo apilado (stack): igual que en el anterior, crearemos algunos modelos de primer nivel; pero luego seleccionaremos uno de segundo nivel, que tomará las predicciones de los de primer nivel como entradas para realizar su propia predicción.
Como primer paso, cargamos y preparamos los datos:
library(C50)
library(modeldata)
data(mlc_churn)
churn <- mlc_churn
# Variables target y predictoras (features)
# Variables target y predictoras (features)
target <- "churn"
predictoras <- names(churn)[names(churn) != target]
# Convertimos factors a integer para que no nos de problemas con svm ni xgbm
for (v in predictoras) {
if (is.factor(churn[, v])) {
newName <- paste0("F_", v)
names(churn)[which(names(churn) == v)] <- newName
churn[, v] <- unclass(churn[, newName])
}
}
set.seed(127)
train_idx <- sample(nrow(churn), 0.9*nrow(churn))
churnTrain <- churn[train_idx,]
churnTest <- churn[-train_idx,]
rm(churn)
library(caret)
set.seed(123)
Vamos a seleccionar ahora un modelo de segundo nivel un poco más complejo entre varios posibles: una red neuronal, un random forest, un extreme gradient boosting y un support vector machine.
Ahora puedo utilizar caret para construir tanto los modelos de primer nivel como los de segundo. Por tanto, puedo validarlos mediante la técnica cross validation que puedo utilizar a partir del train set, sin necesidad de utiliizar un validation set aparte para ello.
Construyamos los modelos de primer nivel:
churn_train <- churnTrain
churn_test <- churnTest
trControl <- trainControl(
# 5-fold Cross Validation
method = "cv",
number = 5,
# Save the predictions for the optimal tuning
# parameters
savePredictions = 'final',
# Class probabilities will be computed along with
# predicted values in each resample
classProbs = TRUE
)
f <- as.formula(paste0(target, "~ ."))
model_rf <- train(f, churn_train[ , c(predictoras, target)],
method = "rf",
trControl = trControl,
tuneLength = 3)
model_svm <- train(f, churn_train[ , c(predictoras, target)],
method = "svmRadial",
trControl = trControl,
tuneLength = 3)
model_xgbm <- train(f, churn_train[ , c(predictoras, target)],
method = "xgbTree",
trControl = trControl,
tuneLength = 3)
Ahora compararíamos la performance y la correlación de los modelos de primer nivel como hemos hecho antes, por eso no vamos a repetirlo.
Pasamos, pues, directamente, a construir los modelos de segundo nivel, en este caso a partir del train_set:
# Utilizamos los modelos de 1er nivel para predecir las probabilidades
# Out-Of-Fold del training set
churn_train$OOF_pred_rf <-
model_rf$pred$yes[order(model_rf$pred$rowIndex)]
churn_train$OOF_pred_svm <-
model_svm$pred$yes[order(model_svm$pred$rowIndex)]
churn_train$OOF_pred_xgbm <-
model_xgbm$pred$yes[order(model_xgbm$pred$rowIndex)]
Hay que hacer notar que siempre debemos emplear en esta fase las predicciones out of bag o out of fold; de otra manera la importancia de los modelos de primer nivel sería tan solo función de lo bien que cada modelo de primer nivel es capaz de “recordar” los datos de entrenamiento.
Ahora ya podemos entrenar los modelos de segundo nivel:
# Predictoras de los modelos de primer nivel para el segundo nivel
predictoras2N <- c('OOF_pred_rf','OOF_pred_svm','OOF_pred_xgbm')
trControl <- trainControl(
# 5-fold Cross Validation
method = "cv",
number = 5,
# Class probabilities will be computed along with
# predicted values in each resample
classProbs = TRUE
)
model_2nn <- train(f, churn_train[ , c(predictoras2N, target)],
method = "nnet",
# Neural nets like scaled and normalized inputs
preProcess = c("center", "scale"),
trace = FALSE,
trControl = trControl,
tuneLength = 3)
model_2rf <- train(f, churn_train[ , c(predictoras2N, target)],
method = "rf",
trControl = trControl,
tuneLength = 3)
## note: only 2 unique complexity parameters in default grid. Truncating the grid to 2 .
model_2svm <- train(f, churn_train[ , c(predictoras2N, target)],
method = "svmRadial",
trControl = trControl,
tuneLength = 3)
model_2xgbm <- train(f, churn_train[ , c(predictoras2N, target)],
method = "xgbTree",
trControl = trControl,
tuneLength = 3)
Y compararlos:
resamps <- resamples(list(nnet = model_2nn, rf = model_2rf,
svm = model_2svm, xgbm = model_2xgbm))
summary(resamps)
##
## Call:
## summary.resamples(object = resamps)
##
## Models: nnet, rf, svm, xgbm
## Number of resamples: 5
##
## Accuracy
## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## nnet 0.9566667 0.9588889 0.9611111 0.9600000 0.9611111 0.9622222 0
## rf 0.9533333 0.9588889 0.9588889 0.9584444 0.9588889 0.9622222 0
## svm 0.9300000 0.9444444 0.9455556 0.9426667 0.9466667 0.9466667 0
## xgbm 0.9522222 0.9588889 0.9588889 0.9613333 0.9666667 0.9700000 0
##
## Kappa
## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## nnet 0.8051083 0.8227781 0.8263506 0.8241705 0.8331061 0.8335095 0
## rf 0.7923647 0.8137584 0.8190217 0.8152334 0.8215434 0.8294790 0
## svm 0.7177700 0.7767303 0.7799847 0.7686728 0.7804878 0.7883909 0
## xgbm 0.7851194 0.8123944 0.8137584 0.8267822 0.8537774 0.8688613 0
bwplot(resamps)
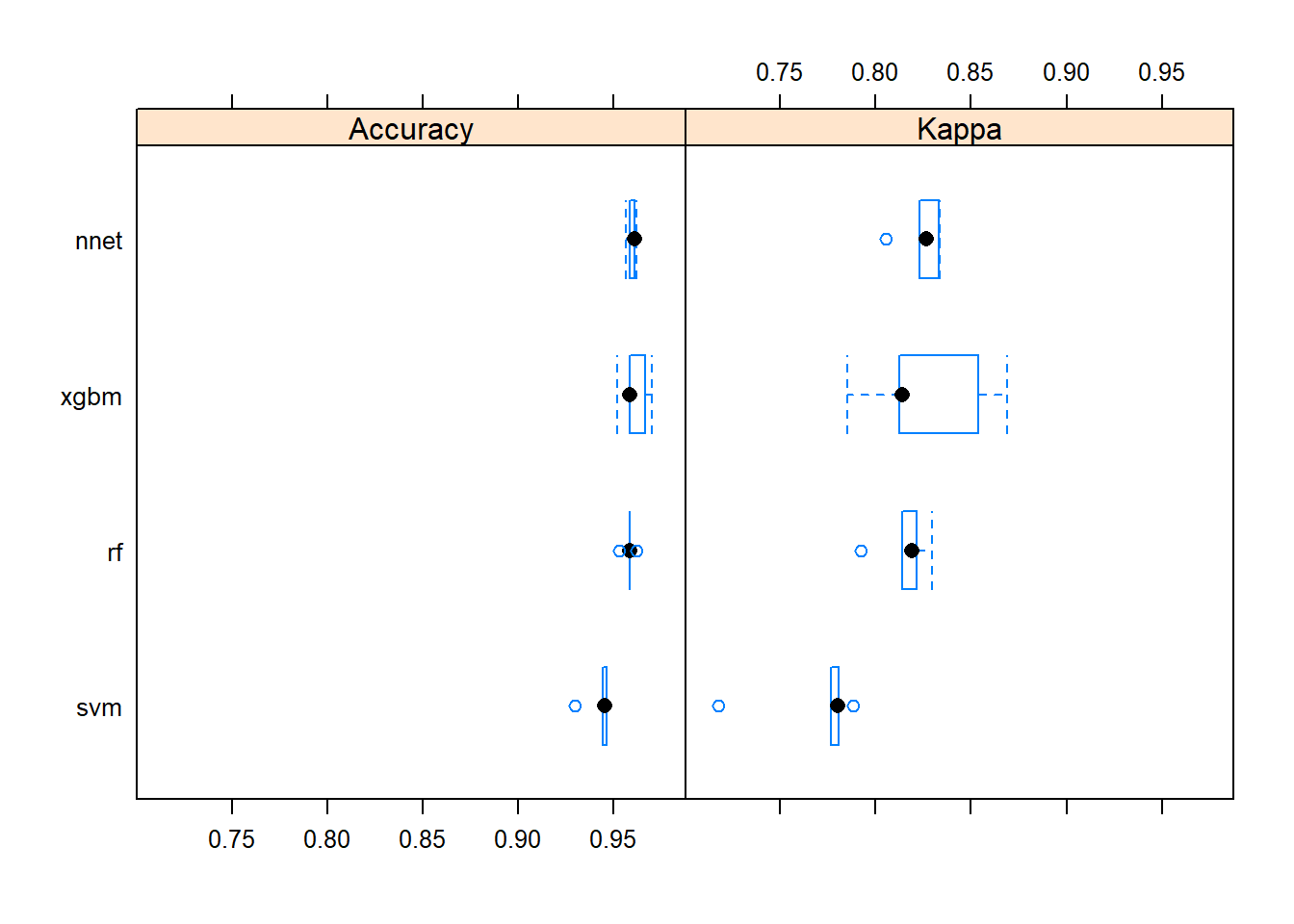
diffs <- diff(resamps)
summary(diffs)
##
## Call:
## summary.diff.resamples(object = diffs)
##
## p-value adjustment: bonferroni
## Upper diagonal: estimates of the difference
## Lower diagonal: p-value for H0: difference = 0
##
## Accuracy
## nnet rf svm xgbm
## nnet 0.001556 0.017333 -0.001333
## rf 1.00000 0.015778 -0.002889
## svm 0.02588 0.07628 -0.018667
## xgbm 1.00000 1.00000 0.04815
##
## Kappa
## nnet rf svm xgbm
## nnet 0.008937 0.055498 -0.002612
## rf 1.00000 0.046561 -0.011549
## svm 0.08275 0.20369 -0.058109
## xgbm 1.00000 1.00000 0.15473
xgbm y random forest son virtualmente indistinguibles.
Como xgbm es ligeramente superior en accuracy y en Kappa a nnet, nos quedaremos con xgbm como modelo final.
Solo nos queda ya comprobar el resultado con el test set:
churn_test$OOF_pred_rf <- predict(model_rf, churn_test[, predictoras],
type = "prob")$yes
churn_test$OOF_pred_svm <- predict(model_svm, churn_test[, predictoras],
type = "prob")$yes
churn_test$OOF_pred_xgbm <- predict(model_xgbm, churn_test[, predictoras],
type = "prob")$yes
churn_test$pred_nn <- predict(model_2xgbm, churn_test[, predictoras2N])
confusionMatrix(churn_test$churn, churn_test$pred_nn)
## Confusion Matrix and Statistics
##
## Reference
## Prediction yes no
## yes 64 18
## no 1 417
##
## Accuracy : 0.962
## 95% CI : (0.9413, 0.977)
## No Information Rate : 0.87
## P-Value [Acc > NIR] : 1.773e-12
##
## Kappa : 0.8488
##
## Mcnemar's Test P-Value : 0.0002419
##
## Sensitivity : 0.9846
## Specificity : 0.9586
## Pos Pred Value : 0.7805
## Neg Pred Value : 0.9976
## Prevalence : 0.1300
## Detection Rate : 0.1280
## Detection Prevalence : 0.1640
## Balanced Accuracy : 0.9716
##
## 'Positive' Class : yes
##
Como veis, unos resultados excelentes, mejores incluso que los de los modelos por separado con el train set.
Por último, deciros que tenéis el código en github.
