Machine Learning Ensembles - y IV
La técnica conocida como bagging consiste en muestrear los datos de entrenamiento de una manera muy concreta llamada bootstrapping y utilizar luego cada muestra así tomada para ajustar sendos modelos (de clasificación o regresión) con los que construir un enesemble.
Así, la estructura del método es muy sencilla: primero, generamos N muestras bootstrap a partir de los datos originales. A continuación utilizamos cada muestra para construir un modelo del ensemble que luego usaremos para realizar una predicción sobre otra muestra diferente. Repetimos el proceso con todas las muestras que hayamos generado y, por último, contamos o promediamos las predicciones para calcular la predicción del ensemble.
Bagging significa Bootstrap + Aggregating. Veamos qué significa cada término.
El Bootstrap
El Bootstrap es una técnica de remuestreo. Como se dice en Kuhn and Jhonson’s “Applied predictive Modeling”:
“Las técnicas de remuestreo se suelen usar para estimar el rendimiento de un modelo y funcionan de manera similar: se toma un subconjunto de muestras para entrenar el modelo y las muestras restantes se usan para estimar su eficacia. En efecto, si repetimos este proceso muchas veces podremos estimar lo”bueno” que es el modelo, promediando, por ejemplo la medida de eficacia que nos interese.
Una muestra bootstrap es una muestra de los datos que se obtiene por extracción aleatoria con reemplazamiento.
Esto significa que, después de extraer de los datos una observación determinada, queda todavía disponible para ulteriores extracciones.
Las muestras bootstrap se construyen del mismo tamaño que el data set original. Por tanto, en cada muestra bootstrap lo más probable es que algunas observaciones aparezcan múltiples veces mientras que otras no estarán presentes.
De las observaciones del data set original no seleccionadas para formar parte de la muestra bootstrap se dice que son observaciones ‘out-of-bag’.
En cada iteración de este remuestreo bootstrap se entrena un modelo a partir de las observaciones seleccionadas de la manera explicada y se usa para predecir a partir de las observaciones ‘out-of-bag’“.

In Rudolph Eric Raspe’s tale, Baron Munchausen had, in one of his many adventurous travels, fallen to th ebottom of a deep lake and just as he was to succumb to his fate he thought to pull himself up by his own BOOTSTRAP. The original version is in German, where Munchausen actually draws himself up by the hair, not the bootstraps.
En el cuento de Rudolph Eric Raspe se relata cómo, en uno de sus viajes de aventuras, el Barón Munchausen cayó con su caballo en una profunda ciénaga y, cuando ya estaba a punto de sucumbir a su fatal destino, se le ocurrió que podía sacarse a sí mismo (¡y a su caballo!) tirando de sus bootstraps, las cinchas o tiradores situadas en la parte posterior de sus botas para facilitar la operación de calzarse. Sin embargo, en la versión original en alemán, Munchausen se sacaba a sí mismo de la ciénaga (¡con su caballo!) tirando de su coleta, como se ve en la ilustración, no de sus bootstraps.
El paquete caret y el Bootstrap
El paquete caret proporciona herramientas para generar muestras bootstrap.
Como en Árboles de decisión (IV) y en Machine Learning Ensembles II y III, usemos los datos sobre rotación de clientes en una operadora para ver un ejemplo:
library(C50)
library(modeldata)
data(mlc_churn)
churn <- mlc_churn
set.seed(127)
train_idx <- sample(nrow(churn), 0.9*nrow(churn))
churnTrain <- churn[train_idx,]
churnTest <- churn[-train_idx,]
dim(churnTrain)## [1] 4500 20Para generar 100 muestras bootstrap lo único que hay que hacer es:
library(dplyr)
library(caret)
NUM_BOOTS_RESAMPS = 100
set.seed(123)
churnBootstrap <- createResample(churnTrain$churn, times = NUM_BOOTS_RESAMPS)
str(churnBootstrap %>% head(10))## List of 10
## $ Resample001: int [1:4500] 1 1 2 5 5 9 13 16 17 18 ...
## $ Resample002: int [1:4500] 1 1 2 2 2 4 5 6 7 7 ...
## $ Resample003: int [1:4500] 1 1 2 2 3 4 4 5 7 7 ...
## $ Resample004: int [1:4500] 2 3 3 3 4 5 5 7 10 13 ...
## $ Resample005: int [1:4500] 1 2 3 4 4 5 6 8 8 9 ...
## $ Resample006: int [1:4500] 1 2 3 3 5 6 7 7 8 9 ...
## $ Resample007: int [1:4500] 9 13 13 14 16 16 16 18 19 21 ...
## $ Resample008: int [1:4500] 3 6 8 8 8 9 10 10 14 14 ...
## $ Resample009: int [1:4500] 1 2 2 2 2 4 6 6 10 11 ...
## $ Resample010: int [1:4500] 1 1 3 3 4 4 5 5 8 8 ...Como se ve, hemos obtenido una lista de 100 elementos, cada uno de los cuales es una muestra bootstrap de los índices de churnTrain$churn.
Nótese también que las longitudes de todas las muestras bootstrap son iguales al número de observaciones (filas) de churnTrain y que en cualquiera de las muestras se dan repeticiones de los índices, lo que es debido a la estrategia de selección con reemplazamiento que se ha seguido para construirlas.
Aggregating
Ahora podemos utilizar cada una de estas muestras bootstrap para construir un modelo que prediga churnTrain$churn. Usaremos los resultados de estos 100 modelos para construir nuestro modelo bagged final.
Para nuestro ejemplo usaremos árboles C5.0 CART:
list_of_models <- lapply(churnBootstrap, function(x) {
C5.0(x = churnTrain[x, -20],
y = churnTrain[x, ]$churn,
trials = 1,
rules = FALSE,
weights = NULL,
control = C5.0Control(),
costs = NULL)
})Ahora ya podemos usar cada modelo para predecir en el test set (en este sencillo ejemplo, la estrategia va a ser: “un modelo, un voto”).
multiPredict <- sapply(list_of_models, predict, churnTest)Y contar los votos para emitir la decisión final:
finalDecision <- apply(multiPredict, 1, function(x) {
if (sum(x == "yes") > sum(x == "no"))
return("yes")
else
return("no")
})
finalDecision <- factor(finalDecision, levels = levels(churnTest$churn))Comprobemos la eficiencia nediante una matriz de confusión:
confusionMatrix(reference = churnTest$churn, data = finalDecision)## Confusion Matrix and Statistics
##
## Reference
## Prediction yes no
## yes 59 2
## no 23 416
##
## Accuracy : 0.95
## 95% CI : (0.9271, 0.9674)
## No Information Rate : 0.836
## P-Value [Acc > NIR] : 3.722e-15
##
## Kappa : 0.7967
##
## Mcnemar's Test P-Value : 6.334e-05
##
## Sensitivity : 0.7195
## Specificity : 0.9952
## Pos Pred Value : 0.9672
## Neg Pred Value : 0.9476
## Prevalence : 0.1640
## Detection Rate : 0.1180
## Detection Prevalence : 0.1220
## Balanced Accuracy : 0.8574
##
## 'Positive' Class : yes
## Sería interesante comparar estos resultados con los obttenidos en Árboles de decisión (IV).
Rendimiento
Lo que si vamos a hacer es comparar la eficiencia del modelo bagging final con el rendimiento de los modelos individuales. Para ello vamos a usar las siguientes funciones:
kpiPlot<- function(kpis, kpi = "Accuracy") {
boxplot(kpis[, kpi],
# ylim = c(0.9995*min(kpis[, kpi]), 1.0005*max(kpis[, kpi]))
main = kpi)
abline(h = kpis["Bagging Model", kpi], col = "red")
}
getPerfKPIs <- function(list_of_models, pred, tgt, finalDecision) {
cms <- lapply(list_of_models, function(x) {
confusionMatrix(data = predict(x, pred), tgt)
})
kpis <-
rbind(as.data.frame(t(sapply(cms, function(x) {x$overal}))),
confusionMatrix(reference = tgt, data = finalDecision)$overall)
kpis <-
cbind(kpis,
rbind(as.data.frame(t(sapply(cms, function(x) {x$byClass}))),
confusionMatrix(reference = tgt, data = finalDecision)$byClass))
rownames(kpis) <- c(sprintf("Modelo %d", 1:NUM_BOOTS_RESAMPS), "Bagging Model")
kpis
}De manera que:
kpis <- getPerfKPIs(list_of_models, churnTest,
churnTest$churn, finalDecision)
par(mfrow = c(3,3))
kpiPlot(kpis, "Accuracy")
kpiPlot(kpis, "Kappa")
kpiPlot(kpis, "Sensitivity")
kpiPlot(kpis, "Specificity")
kpiPlot(kpis, "Pos Pred Value")
kpiPlot(kpis, "Neg Pred Value")
kpiPlot(kpis, "Precision")
kpiPlot(kpis, "Recall")
kpiPlot(kpis, "F1")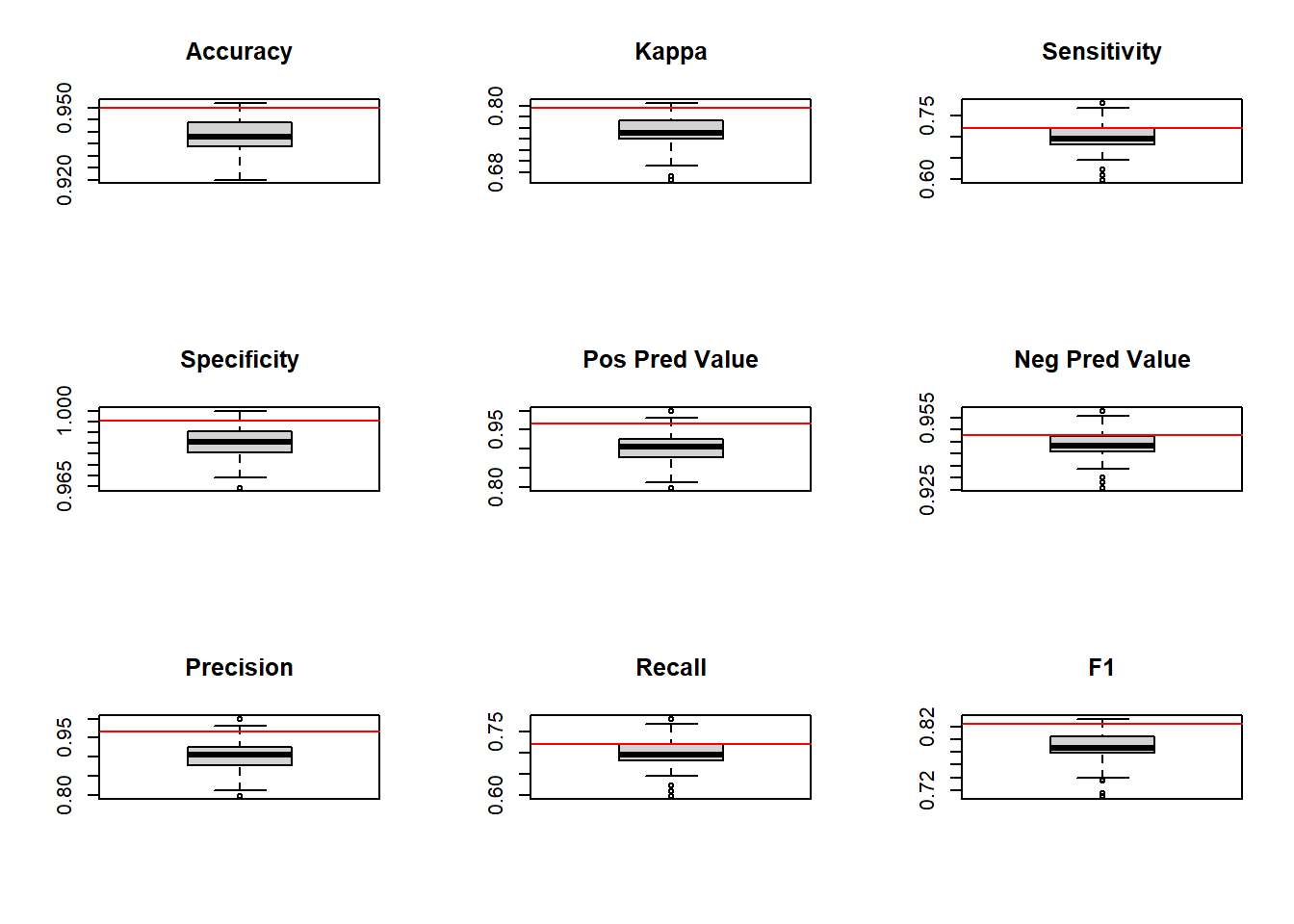
par(mfrow = c(1,1))Las líneas rojas indican la ubicación de las medidas correspondientes a los diferentes KPIs para el modelo bagged; las boxplots se refieren al mismo KPI según esté distribuido en los 100 modelos individuales generados.
Como se ve, la línea roja, como poco, está siempre en la zona de mejores resultados.
Los modelos bagging reducen la varianza de la predicción pero suelen aportar mejoras poco impresionantes en cuanto a la eficacia predictiva.
En su forma básica, la elección que podemos hacer para construir modelos bagging es el número de muestras bootstrap que agregar. A menudo se aprecia un descenso importante en la mejora predictiva al aumentar el número de iteraciones: la mayor parte de la mejora se obtiene con un número relativamente pequeño de árboles (m < 10).
Aunque la técnica bagging normalmente mejore la eficacia predictiva de modelos poco estables, hay un par de reflexiones que considerar sobre ellos:
Primero, los costes en cuanto a recursos de computación y memoria aumentan al aumentar el número de muestras bootstrap. Esto puede mitigarse si tenemos acceso a algún tipo de computación paralela, ya que los procesos bagging son fácilmente paralelizables: cada muestra es independiente de las demás y, por tanto, cada modelo es independiente de las otras muestras y modelos, lo que significa que podemos construirlos por separado y solo juntarlos al final para generar la predicción.
La otra desventaja de esta técnica es que los modelos bagged sacrifican interpretabilidad en aras de la eficiencia.

