Multicolinealidad, inferencia y predicción
A menudo oimos lo mala que es la multicolinealidad en los modelos de regresión. En este artículo vamos a ver en qué consiste y cuáles son sus efectos, lo que nos llevará, curiosamente, a otras disquisiciones habituales:
- ¿Qué diferencia hay entre inferencia y predicción?
- ¿Qué enfoque es mejor?
- Machine Learning: lo meto todo en la coctelera sin darle muchas vueltas a la cabeza y pruebo muchos tipos de modelo y consjuntos de hperparámetros.
- Estadístico clásico: construir un modelo exige ponerle mucha cabeza.
Y el recorrido nos conducirá, inevitablemente, a plantearnos qué papel juega la causalidad en todo esto. Y si, lo has adivinado, al final saldrá también aquello de “correlación no implica causalidad”.
Vamos allá. Lo haremos metiendo las manos directamente en harina. Vamos a plantearnos un problema que podría ser real, pero lo haremos con datos cocinados. Es este: queremos investigar qué relación hay entre el consumo de café, el de tabaco y el cáncer.
Para “fabricarnos” los datos nos aprovecharemos de que sabemos la respuesta, tras muchos años de investigación por los científicos. Y la respuesta es que, aunque en algún momento de la historia se sospechó que el café causaba cáncer, tan solo se debía a que las personas que siguen determinado estilo de vida consumen café Y tabaco. Obviamente el cancerígeno es el tabaco.
“Fabricaremos” primero los datos y luego haremos como que no lo sabemos.
Ya que lo conocemos, el modelo causal pinta así:
library(tidyverse)
library(dagitty)
dag_OK_cafe_tabaco <-
dagitty::dagitty('dag{
cafe <- estilo_de_vida -> tabaco -> cancer
cancer [outcome, pos="0,2"]
cafe [exposure, pos="-2,0"]
tabaco [exposure, pos="2, 0"]
estilo_de_vida [unobserved, pos="0,-2"]}')
plot(dag_OK_cafe_tabaco)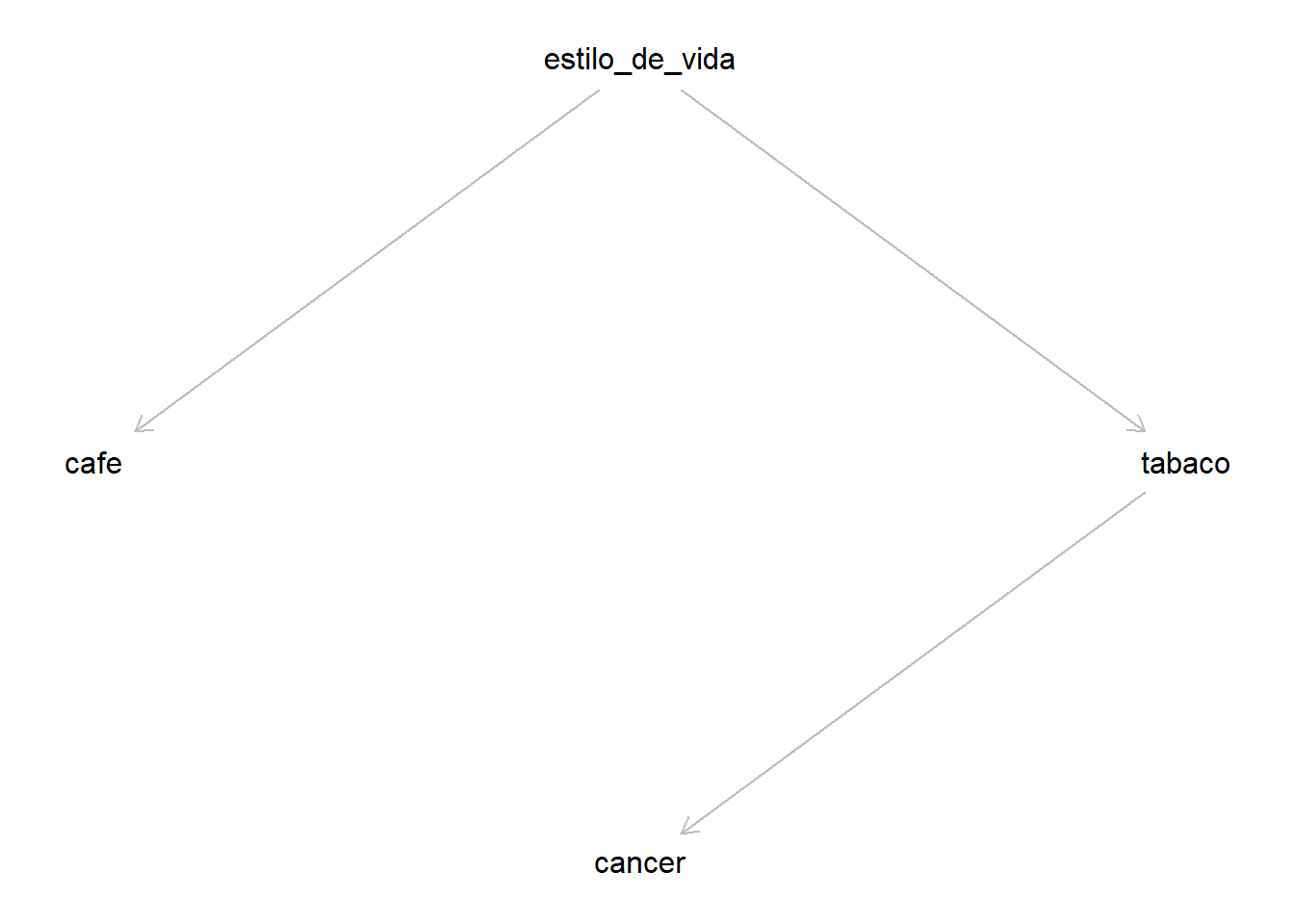
Podemos simular los datos de esta manera:
N <- 1000
estilo_de_vida <- seq(-100, 100, length.out = N)
set.seed(2021)
# estilo_de_vida causa consumo de café
cafe <- rnorm(N, .9 * estilo_de_vida, 10)
# estilo_de_vida causa también consumo de tabaco
tabaco <- rnorm(N, .7 * estilo_de_vida, 15)
# El consumo de tabaco causa cáncer
cancer <- rnorm(N, 0.5 * tabaco, 20)
# Lo juntamos todo
d <- tibble(estilo_de_vida, cafe, tabaco, cancer)
idx_train <- caret::createDataPartition(d$cancer, p = .8, list = FALSE)
d_train <- d[idx_train, ]
d_test <- d[-idx_train, ]Vale, ya tenemos nuestros datos. Hagamos ahora como que nos los encontramos por primera vez sin saber cómo se han generado. Lo primero sería explorar los datos “observables”. Por ejemplo:
# El estilo_de vida no es "observable".
psych::pairs.panels(d_train %>% select(-estilo_de_vida))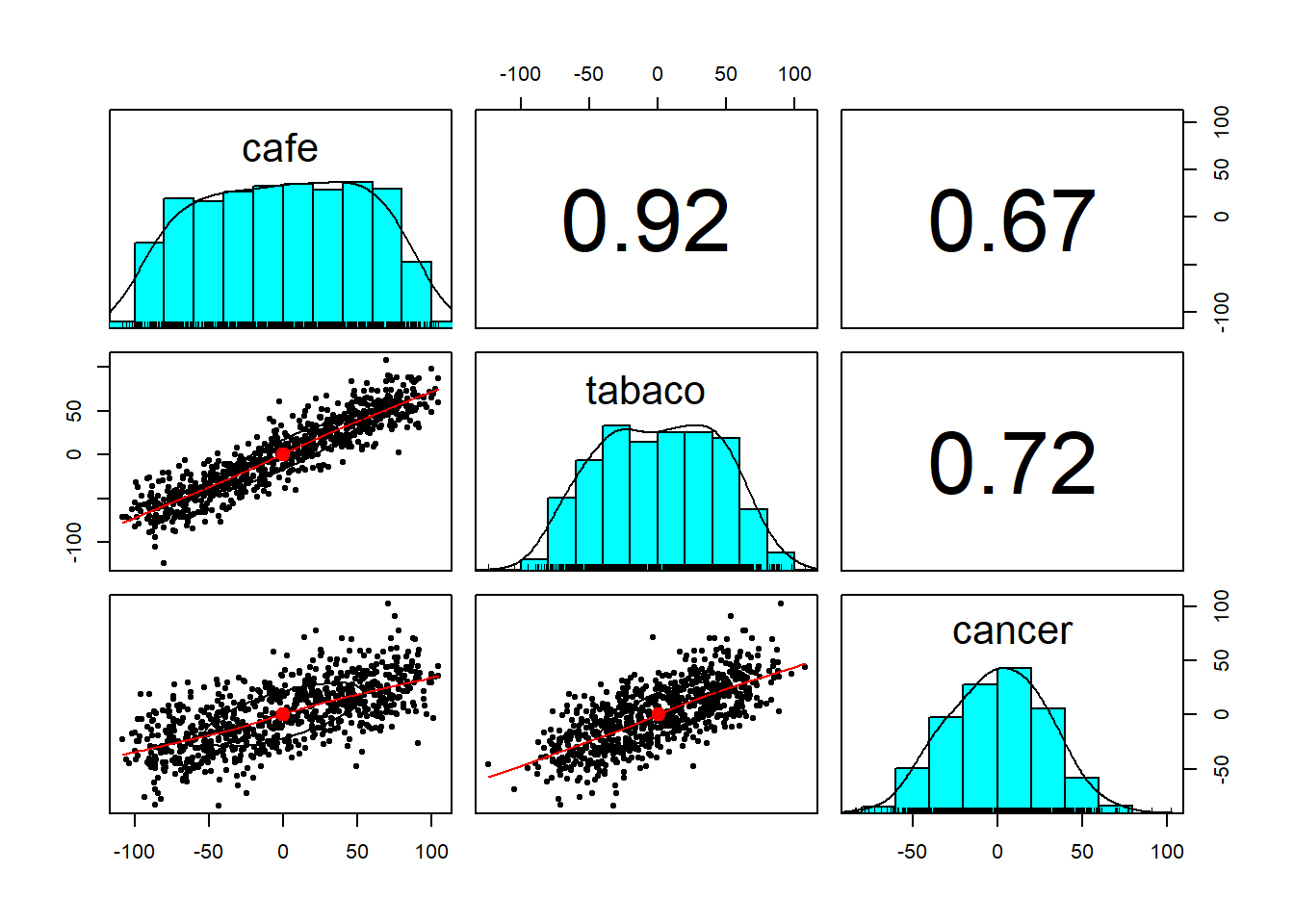
Vemos una alta correlación tanto entre tabaco y cáncer como entre café y cáncer.
Podríamos hipotetizar este modelo causal:
dag_Hipo_cafe_tabaco <-
dagitty::dagitty('dag{
tabaco -> cancer <- cafe
cancer [outcome, pos="0,2"]
cafe [exposure, pos="-2,0"]
tabaco [exposure, pos="2, 0"]}')
plot(dag_Hipo_cafe_tabaco)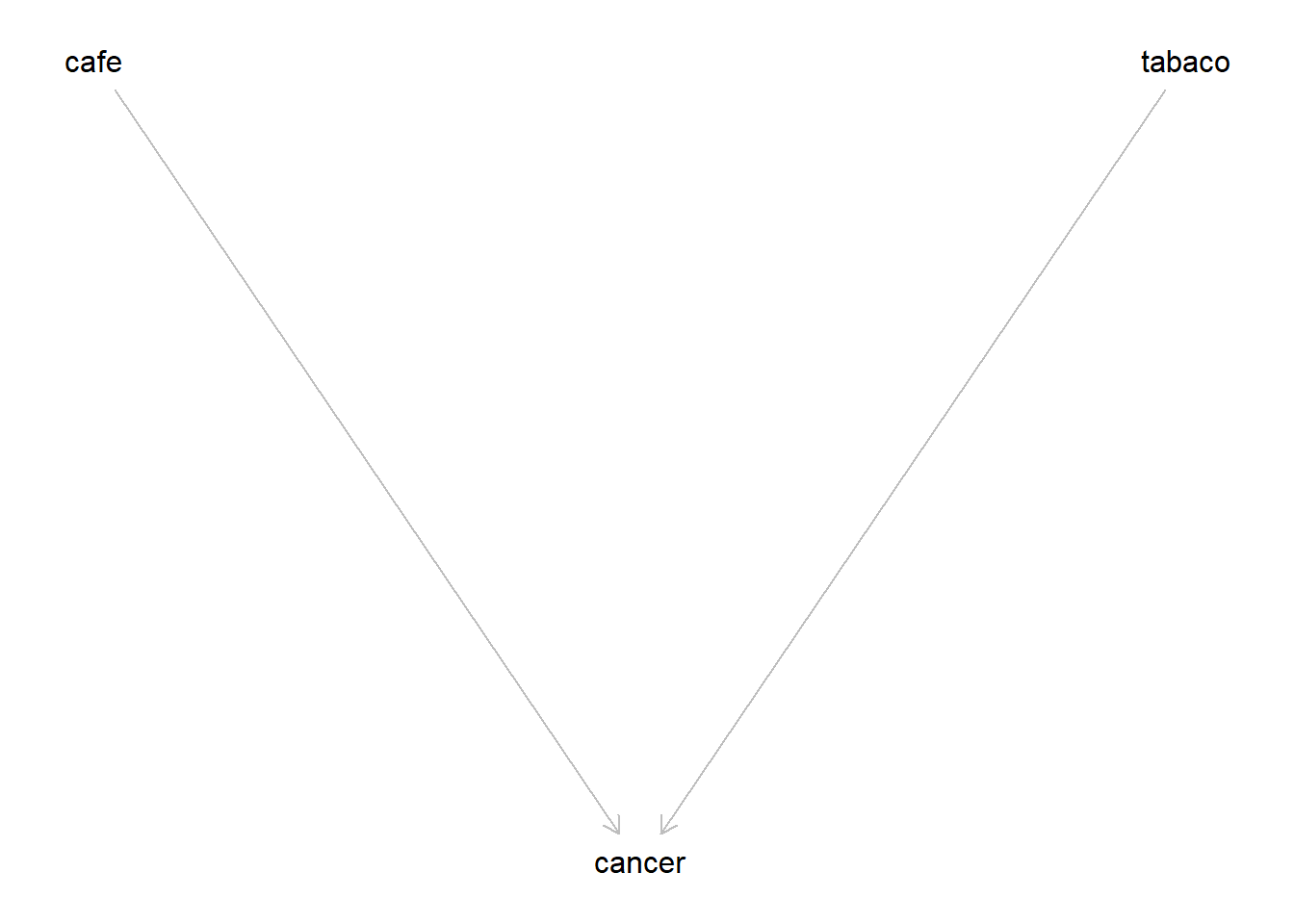
Y construir por tanto una regresión con tabaco y cafe como variables
explicativas:
lm_cafe_tabaco <- lm(cancer ~ cafe + tabaco, d_train)
summary(lm_cafe_tabaco)##
## Call:
## lm(formula = cancer ~ cafe + tabaco, data = d_train)
##
## Residuals:
## Min 1Q Median 3Q Max
## -68.354 -14.442 -0.442 13.902 73.135
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.05810 0.71782 0.081 0.936
## cafe 0.01311 0.03409 0.385 0.701
## tabaco 0.47457 0.04220 11.246 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 20.29 on 797 degrees of freedom
## Multiple R-squared: 0.5217, Adjusted R-squared: 0.5205
## F-statistic: 434.6 on 2 and 797 DF, p-value: < 2.2e-16Vaya, tabaco parece una variable significativa, pero cafe no…
¿Cuál es su capacidad de predicción? Veamos:
Metrics::mape(d_test$cancer, predict(lm_cafe_tabaco, d_test))## [1] 1.561191Y ¿si solo usáramos tabaco?
lm_tabaco <- lm(cancer ~ tabaco, d_train)
summary(lm_tabaco)##
## Call:
## lm(formula = cancer ~ tabaco, data = d_train)
##
## Residuals:
## Min 1Q Median 3Q Max
## -68.439 -14.288 -0.309 13.844 73.383
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.04985 0.71712 0.07 0.945
## tabaco 0.48949 0.01660 29.50 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 20.28 on 798 degrees of freedom
## Multiple R-squared: 0.5216, Adjusted R-squared: 0.521
## F-statistic: 870 on 1 and 798 DF, p-value: < 2.2e-16Metrics::mape(d_test$cancer, predict(lm_tabaco, d_test))## [1] 1.569951Era previsible: la variable tabaco sigue siendo significativa y la predicción sobre datos de test es casi igual.
Por cierto: ¿te has fijado que los coeficientes de tabaco y cafe del primer
modelo suman más o menos lo mismo que el coeficiente de tabaco en el segundo?
Vaya, vaya…
Pero ¡un momento! ¿Y si hacemos un modelo solo con café? A ver….
lm_cafe <- lm(cancer ~ cafe, d)
summary(lm_cafe)##
## Call:
## lm(formula = cancer ~ cafe, data = d)
##
## Residuals:
## Min 1Q Median 3Q Max
## -68.124 -14.445 -1.265 14.513 76.619
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.06791 0.69313 0.098 0.922
## cafe 0.36781 0.01297 28.349 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 21.92 on 998 degrees of freedom
## Multiple R-squared: 0.4461, Adjusted R-squared: 0.4455
## F-statistic: 803.7 on 1 and 998 DF, p-value: < 2.2e-16¡Anda! Ahora cafe es significativa casi igual que tabaco antes…
Metrics::mape(d_test$cancer, predict(lm_cafe, d_test))## [1] 1.61489Y no predice mucho peor…
Resumiendo: el modelo que hemos hipotetizado, con dos variables explicativas
- cafe y tabaco - fuertemente correlacionadas entre si, sufre de colinealidad:
observamos como una variable -tabaco “expulsa” a la otra - cafe.
La explicación es que el modelo que estamos usando no es correcto causalmente.
Esto no es grave a efectos meramente predictivos, como hemos visto. Si lo único que queremos es predecir, no hace falta que le demos muchas vueltas al modelo. Podemos emplear la táctica machine learning - meter todas las variables y construir el mejor modelo - y ¡hala! a predecir.
Pero si es grave desde un punto de vista inferencial - entender cómo
funcionan las cosas -, ya que cuando usamos
las dos variables explicativas a la vez, debido a la colinealidad el efecto de la que realmente causa
cáncer - tabaco - aparece atenuado por la presencia de cafe.
Y esto es particularmente grave si quiero usar el modelo par a intervenir. Me llevaría a pensar que reduciendo el consumo de café disminuiría un poco el cáncer.
Dicho de otro modo, si queremos usar el modelo para entender lo que sucede o, con más razón, para intervenir, tendremos que usar más la cabeza para plantear un modelo causalmente correcto.
Pero, si cafe no es causa de cancer ¿por qué funciona bien el modelo que
la usa como única variable predictiva? Si solo miramos ese modelo parece que
cafe si es causa de cancer, ¿no?
La razón es que hay un camino no causal entre cafe y cancer en el modelo causal
correcto (fíjate en el sentido de las flechas para ver que es un camino no causal:
cancer <- tabaco <- estilo_de_vida -> cafe.
La existencia de ese camino produce una correlación entre cafe y cancer. Ya
lo ves, hay correlación pero no causalidad. Y ello es posible gracias a la existencia
de la variable estilo_de_vida (no observable, en este caso), que actúa aquí
como confounder.
Sin embargo, esa asociación entre cafe y cancer se interrumpe al incluir
tabaco en el modelo. En efecto, el camino esiilo_de_vida -> tabaco -> cancer
es lo que se conoce como cadena (chain). Es un camino transitable siempre que no condicionemos
(incluyamos en el modelo) la variable central tabaco, en cuyo caso el camino deja
de ser transitable.
En este modelo hay otra figura importante, la bifurcación (fork) cafe<- estilo_de_vida -> tabaco.
Se trata también de un camino transitable mientras no condicionemos en la variable central.
Como en este caso no podemos hacerlo, ya que estilo_de_vida no es observable,
on podemos usarla para cerrar el camino entre cafe y cancer.
Bueno, pero estamos haciendo algo de trampa ¿no? Todo esto lo sabemos de partida
porque hemos creado el modelo. ¿Qué tendríamos que hacer si queremos hacer inferencia
y solo tuviéramos los datos observables? Pues usar la cabeza. Eso siginifica que
partimos de una hipótesis inicial (cafe-> cancer <- tabaco) y - esto es
lo más importante - de la estructura causal de nuestro
hipotético modelo podemos deducir consecuencias comprobables en los datos
relativas a las independencias tanto marginales como condicionales entre las
variables del modelo. E
sto lo podemos utilizar para contrastar la validez
del modelo que estemos planteando como hipótesis.
Nuestro modelo hipotético tiene la forma del tercer elemento a considerar en un gráfico causal DAG (Directed Acyclic Graph): se trata de un colisionador (collider). A diferencia de los 2 anteriores, la cadena y la bifurcación, el colisionador por defecto no es transitable, está cerrado. Pero se abre al condicionar en la variable central.
Por lo tanto, deducimos del gráfico DAG que, de ser correcto el modelo:
cafeytabacodeberían ser independientes (y, por lo tanto, no correladas) entre ellas;- A no ser que condicionemos en
cancer, en cuyo casocafeinfluiría entabacoa través decancerlo que provocaría una correlación entrecafeytabaco, que serían ahora dependientes entre si condicionalmente acancer
Y estas dos deducciones son comprobables en los datos. De hecho, ya hemos visto que la primera no se cumple, luego nuestro hipotético modelo no es correcto.
Nos preguntaríamos entonces qué induce la correlación entre cafe y tabaco e
identificaríamos como causa probable la existencia de una variable no observada
que influye a la vez sobre tabaco y cafe. Una bifurcación, vamos.
