Causalidad: ¿machine learning o modelos "clásicos"?
En este post vamos a mezclar R con Python. Los gráficos de modelos causales
están hechos con el paquete dagitty.
El resto con Python. Este blog se edita con blogdown
y RStudio nos permite
crear archivos Rmarkdown mezclando R y Python gracias al paquete reticulate.
Vídeo introductorio:
library(tidyverse, quietly = TRUE)## Warning: package 'readr' was built under R version 4.1.2library(dagitty)
library(reticulate)
Sys.setenv(RETICULATE_PYTHON="")
options(reticulate.repl.quiet = TRUE)
reticulate::use_condaenv("ml-course-edix")import warnings
warnings.filterwarnings('ignore')
import numpy as np
import statsmodels.api as sm
import pandas as pd
from sklearn.metrics import mean_absolute_errorBifurcación (fork)
¿Qué es un confounder? Básicamente, una variable aleatoria oculta que es la causa de otras variables aleatorias visibles en las que “induce” una dependencia.
dag_fork <- dagitty('dag {
bb="0,0,1,1"
X [pos="0.3,0.2"]
Y [pos="0.5,0.2"]
Z [pos="0.4,0.15"]
Z -> X
Z -> Y
}')
plot(dag_fork)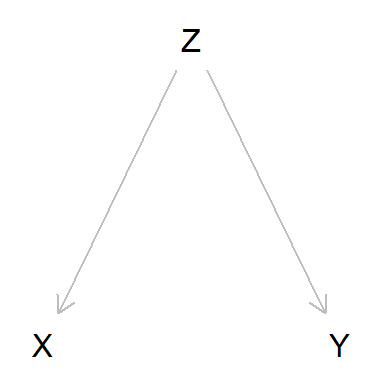
Esta estructura causal se denomina fork o bifurcación: Z es
la causa tanto de X como de Y.
Veámoslo con un ejemplo sintético.
N = 1000
np.random.seed(2022)
Z = np.random.normal(0, 1, N)
X = np.random.normal(Z, 1, N)
Y = np.random.normal(Z, 1, N)
fork_df = pd.DataFrame({'X':X, 'Y':Y, 'Z': Z})Las v.a.’s X e Y se generan a partir de Z (nuestro confounder).
Esa es la razón de que X e Y no sean independientes. En efecto, si
fueran independientes su correlación tendría que ser nula, lo que no es
el caso:
fork_df.corr()## X Y Z
## X 1.000000 0.499050 0.692473
## Y 0.499050 1.000000 0.702374
## Z 0.692473 0.702374 1.000000Si no disponemos de la variable confounder Z, basándonos en la
correlación entre X e Y el modelo que construiríamos sería este:
fork_lm = sm.OLS(fork_df['Y'], fork_df['X']).fit()
print(fork_lm.params)## X 0.504956
## dtype: float64print(fork_lm.pvalues)## X 3.244596e-64
## dtype: float64En el que X , claro, sale significativa. Esto explica por qué
podemos predecir Y a partir de X. Pero, como no somos
conscientes de la existencia de Z y su relación causal con X e Y:
- Nos equivocaremos si concluimos que
Xes causa deY. - Y erraremos también si prescribimos que una intervención sobre
Xnos permitirá modificarY.
En definitiva, queda claro que podemos predecir sin tener en cuenta la estructura causal, es decir, sólo a partir de la asociación inducida por el confounder.
Pero lo que no conseguiremos sin tener en cuenta las relaciones causales es ni entender cómo funcionan las cosas (inferencia) ni prescribir correctamente para poder intervenir con éxito sobre la realidad.
Resumen - Bifurcación (fork)
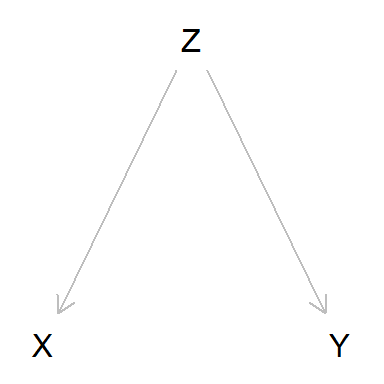
Al analizar los datos disponibles (X e Y) vemos que correlan. Por
tanto probamos el modelo \(Y \sim X\) y comprobamos que funciona bien.
El peligro de este fork es que pensemos que X es causa de Y. Si
intentáramos modificar Y interviniendo en Xno conseguiríamos nada.
Colinealidad
También es muy habitual encontrar variables explicativas correlacionadas, lo que produce problemas de colinealidad en las regresiones lineales. Veamos por ejemplo esta estructura causal:
dag_colin <- dagitty('dag {
bb="0,0,1,1"
X1 [pos="0.3,0.2"]
X2 [pos="0.4,0.2"]
Z [pos="0.35,0.15"]
Y [pos="0.3,0.3"]
Z -> X1
Z -> X2
X1 -> Y
}')
plot(dag_colin)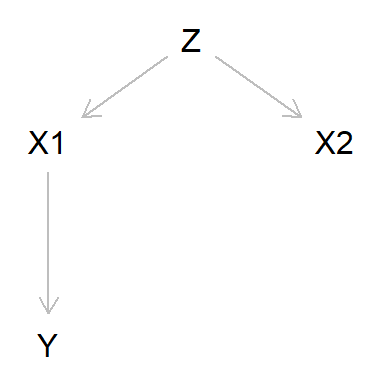
Fabriquemos un ejemplo sintético.
np.random.seed(2022)
Z = np.linspace(-100, 100, N)
X1 = np.random.normal(.9*Z, 10, N)
X2 = np.random.normal(.7*Z, 15, N)
Y = np.random.normal(0.5*X1, 20, N)
colin_df = pd.DataFrame({'X1':X1, 'X2':X2, 'Y':Y, 'Z': Z})print(colin_df.corr())## X1 X2 Y Z
## X1 1.000000 0.919292 0.801721 0.982527
## X2 0.919292 1.000000 0.743092 0.937735
## Y 0.801721 0.743092 1.000000 0.788665
## Z 0.982527 0.937735 0.788665 1.000000Al haberlas creado asociadas (es decir, dependientes), la correlación
entre X1 y X2 no tiene por qué ser \(0\) - como podemos comprobar
arriba, en nuestro caso no lo es en absoluto.
Sin embargo, X1 y X2 presentan el problema de la colinealidad: ambas
correlan entre ellas pero también con Y aunque X2 no ha intervenido
para nada en la generación de Y: se trata de una correlación espúrea
inducida por el confounder Z.
Si incluimos ambas en la regresión:
colin_lm = sm.OLS(colin_df['Y'], colin_df[['X1', 'X2']]).fit()
print(colin_lm.params)## X1 0.479845
## X2 0.030429
## dtype: float64print(colin_lm.pvalues)## X1 4.473266e-51
## X2 4.128670e-01
## dtype: float64X2 no sale significativa: lo que nos está diciendo es que el efecto
causal de X2 sobre X1 es nulo.
(Por cierto, nótese como la suma de los coeficientes es casi igual al número que hemos usado al generar los datos - \(0.5\) -)
En cualquier caso, veamos cómo predice este modelo:
y_true = colin_df['Y']
y_pred = colin_lm.predict()
print(mean_absolute_error(y_true, y_pred))## 15.774561523819266Pero atención: si hacemos sendos modelos univariable resulta que
predicen más o menos igual (de hecho, a veces podría ¡hasta predice
mejor el modelo con X2!)
Modelo solo con X1:
colin_lm_X1 = sm.OLS(colin_df['Y'], colin_df[['X1']]).fit()
print(colin_lm_X1.params)## X1 0.502529
## dtype: float64print(colin_lm_X1.pvalues)## X1 1.640557e-225
## dtype: float64y_pred = colin_lm_X1.predict()
print(mean_absolute_error(y_true, y_pred))## 15.790672097189905Como era de esperar, X1 sale significativa. Éste es el mejor modelo (y
con coeficiente \(0.5\))
Modelo solo con X2:
colin_lm_X2 = sm.OLS(colin_df['Y'], colin_df[['X2']]).fit()
print(colin_lm_X2.params)## X2 0.57437
## dtype: float64print(colin_lm_X2.pvalues)## X2 1.768978e-176
## dtype: float64X2 ahora sale significativa…
y_pred = colin_lm_X2.predict()
print(mean_absolute_error(y_true, y_pred))## 17.559263999690536… y el error no está muy lejos de de los 2 anteriores.
Resumen - Colinealidad
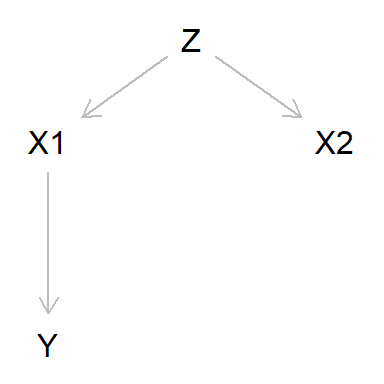
En este caso hemos analizado los datos disponibles (X1, X2 e Y ) y
hemos encontrado correlaciones entre los 3, así que hemos probado el
modelo \(Y \sim X1 + X2\). Encontramos que en el modelo X2 no es
significativa. Lo normal es que pensemos, en este caso acertadamente,
que debemos excluir X2 del modelo. Si no lo hiciéramos, el modelo
seguiría prediciendo Y razonablemente bien, pero nos llevaría a
estimar erróneamente el efecto sobre Y al intervenir en X2.
Otro peligro sería que no dispusiéramos de los datos X1. En ese caso
probaríamos el modelo \(Y \sim X2\) y comprobaríamos que ahora X2
funciona bien. Si intentáramos influir en Y interviniendo sobre X2,
fracasaríamos. Sin embargo, si solo queremos predecir Y, el modelo
funcionaría razonablemente bien.
Cadenas (Chains)
Otro caso interesante es el de las cadenas (chains).
Se trata de situaciones en las que hay una causa X de otra causa
intermedia Y que finalmente causa Z.
dag_chain <- dagitty('dag {
bb="0,0,1,1"
X [pos="0.3,0.2"]
Y [pos="0.4,0.2"]
Z [pos="0.5,0.2"]
X -> Y
Y -> Z
}')
plot(dag_chain)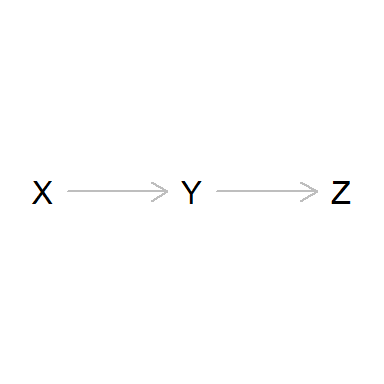
Creemos algunos datos sintéticos:
np.random.seed(2022)
X = np.linspace(-100, 100, N)
Y = np.random.normal(.9*X, 10, N)
Z = np.random.normal(0.5*Y, 20, N)
chain_df = pd.DataFrame({'X':X, 'Y':Y,'Z': Z})Claramente hay asociaciones causales directas entre X e Y y entre
Y y Z; pero también hay una relación causal indirecta entre Xy
Z. Esto explica las correlaciones entre las 3 variables:
print(chain_df.corr())## X Y Z
## X 1.000000 0.982527 0.786870
## Y 0.982527 1.000000 0.797378
## Z 0.786870 0.797378 1.000000Sin embargo, veamos lo que pasa al incluir tanto X como Y en un
modelo explicativo de Z:
chain_lm_X_Y = sm.OLS(chain_df['Z'], chain_df[['X', 'Y']]).fit()
print(chain_lm_X_Y.params)## X 0.056122
## Y 0.436255
## dtype: float64Aunque claramente hay una relación causal entre X y Z, resulta que
ahora X no sale significativa en el modelo.
¿Qué está pasando? Pues que en una chain condicionar sobre la variable
intermedia “bloquea” el efecto de X sobre Y, “cierra el camino”
entre ambas.
Si queremos conocer el efecto total (que es indirecto) de X sobre Z
no debemos incluir Yen el modelo para que el camino entre Xy
Zquede expedito:
chain_lm_X = sm.OLS(chain_df['Z'], chain_df[['X']]).fit()
print(chain_lm_X.params)## X 0.450068
## dtype: float64print(chain_lm_X.pvalues)## X 1.360570e-211
## dtype: float64Resumen - Cadenas (chains)
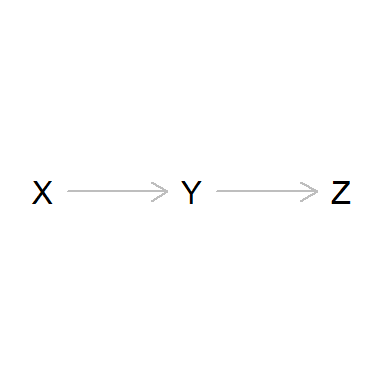
Al analizar los datos disponibles (X, Y, Z) hemos descubierto que
correlan bien entre ellos, así que hemos probado el modelo \(Z \sim X+Y\).
Pero entonces descubrimos que X sale no sigificativa.
El peligro es que, en consecuencia, pensemos que X no tiene efecto
sobre Z. Si queremos conocer su efecto sobre Z debemos excluir Y
del modelo.
Colisionadores (Colliders)
Por último, veamos el caso en que dos variables independientes entre sí son causa simultánea de otra tercera.
dag_collider <- dagitty('dag {
bb="0,0,1,1"
X [pos="0.3,0.15"]
Y [pos="0.5,0.15"]
Z [pos="0.4,0.2"]
X -> Z
Y -> Z
}')
plot(dag_collider)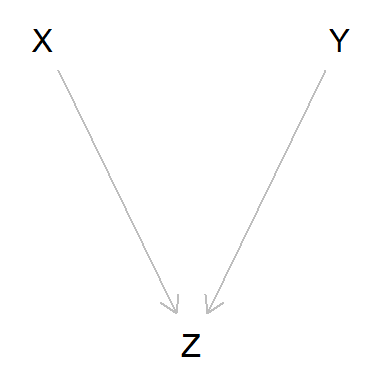
Simulemos los datos:
np.random.seed(2022)
X = np.random.normal(0, 10, N)
Y = np.random.normal(0, 10, N)
Z = np.random.normal(-0.9*X + 0.5*Y, 1, N)
collider_df = pd.DataFrame({'X':X, 'Y':Y,'Z': Z})print(collider_df.corr())## X Y Z
## X 1.000000 -0.031899 -0.871237
## Y -0.031899 1.000000 0.509009
## Z -0.871237 0.509009 1.000000Aquí, claro, no hay correlación entre X e Y; pero cada una de ellas
correlaciona con Z porque ambas son causa de Z.
Supongamos que queremos un modelo para Y. Pensando en términos de
correlación, esperaríamos que X no debería estar en ese modelo.
En efecto, intentamos explicar Y a partir de X:
collider_lm_X = sm.OLS(collider_df['Y'], collider_df[['X']]).fit()
print(chain_lm_X.params)## X 0.450068
## dtype: float64print(collider_lm_X.pvalues)## X 0.317034
## dtype: float64X no es significativa. Lógico ¿no? ya que creamos X e Y de manera
independiente.
Con la misma lógica basada en las correlaciones, pensaríamos que el
modelo debería usar xolo Z:
collider_lm_Z = sm.OLS(collider_df['Y'], collider_df[['Z']]).fit()
print(collider_lm_Z.params)## Z 0.487921
## dtype: float64print(collider_lm_Z.pvalues)## Z 4.786561e-67
## dtype: float64Y, claro, Z sale significativa. Este modelo predeciría bien y pero,
como sabemos cómo se han generado los datos, está claro que intervenir
en Z no tendría efecto en Y.
Por último, ¿y si incluimos tanto X como Y en el modelo?
collider_lm_X_Z = sm.OLS(collider_df['Y'], collider_df[['X', 'Z']]).fit()
print(collider_lm_X_Z.params)## X 1.723143
## Z 1.914652
## dtype: float64print(collider_lm_X_Z.pvalues)## X 0.0
## Z 0.0
## dtype: float64¡Vaya! Ahora no solo sale que Z es significativa (esto es normal
porque hay una relación entre Z e Y: Y es causa de Z), ¡sino que
X también sale significativa!
Este modelo también serviría para predecir, pero no para intervenir.
¿Por que es ahora significativa X? Esto sucede porque, al contrario de
lo que ocurría con la chain, al incluir la variable intermedia en el
modelo hemos abierto el camino entre X e Y:
- Condicionar en la variable intermedia en una chain cierra el camino entre las variables de los extremos, que inicialmente está cerrado.
- Por contra, condicionar sobre la variable intermedia en un collider abre el camino entre las variables de los extremos, que inicialmente está abierto.
Resumen - Colisionadores (colliders)
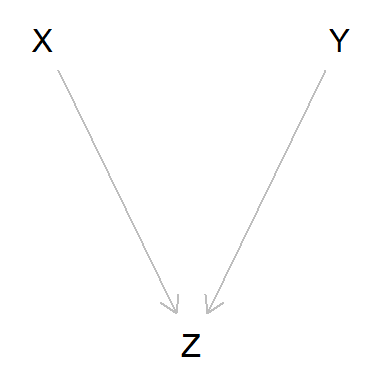
Al analizar los datos disponibles (X, Y, Z) hemos visto que Y
correla zon Z pero no con X. Esto induce a probar el modelo
\(Y \sim Z\), en el que Z sale significativa. Por supuesto, el modelo no
explica Y causalmente, así que intervenir sobre Z no produciría
efecto en Y . Pero el modelo serviría para predecir Y a partir de
Z . Además, si se nos ocurre incluir X también (\(Y \sim Z + X\)),
resulta que tanto X como Z salen significativas. Intervenir en X o
Z tampoco tendría efecto en Y pero como modelo predictivo sí
funcionaría.
Conclusión
Usar un modelo causalmente incorrecto (es decir, creado basándonos solo en las correlaciones) no es un problema a efectos meramente predictivos, como hemos visto. Si lo único que queremos es predecir, no hace falta que le demos muchas vueltas al modelo. Podemos emplear la táctica machine learning - meter todas las variables, buscar el modelo que mejor prediga - y ¡hala! a predecir.
Pero si es un problema desde un punto de vista inferencial - entender cómo funcionan las cosas -, ya que, a efectos explicativos, podemos terminar con una idea errónea de qué causa qué. Y esto es particularmente grave si queremos usar el modelo para intervenir.
Si queremos explicar y/o intervenir tenemos que poner más cabeza en el modelo, empleando metodologías que tengan en cuenta la causalidad para crear modelos causalmente correctos.
